Introduction to Biophysics

Course Outline: PHY 535 (Biophysics) (2 units)

I. Introduction to Biophysics (1 week)

• Definition and scope of biophysics
• Importance of biophysics in biological sciences and medicine

II. Thermodynamic Principles in Biology (2 weeks)

• Laws of thermodynamics (Zeroth, First, Second and Third Laws)
• Enthalpy, entropy, and free energy
• Applications of thermodynamics to biological systems (e.g., enzyme kinetics, membrane transport)

III. Energy Transfer in Living Systems (2 weeks)

• Different forms of energy (kinetic, potential, chemical, etc.)
• Energy transfer mechanisms in biological systems (e.g., radiation, conduction, convection)
• Role of ATP in cellular energy transfer

IV. Bioelectricity (2 weeks)

• Ion channels and their properties
• Action potentials and nerve impulse transmission
• Electrical properties of cells (membrane potential, resting potential)
• Electrocardiogram (ECG) and Electroencephalogram (EEG) (brief introduction)

V. Applications of Ultrasound in Biology and Medicine (1 week)

• Principles of ultrasound generation and propagation
• Medical applications of ultrasound (e.g., imaging, therapy)
• Bioeffects of ultrasound

VI. Fluid Flow and Viscosity in Biological Systems (1 week)

• Properties of fluids (viscosity, density, shear stress)
• Blood flow and its regulation
• Applications of fluid dynamics in physiology (e.g., blood circulation, respiration)

VII. Pressure and its Applications in Biology and Medicine (1 week)

• Blood pressure and its measurement
• Osmotic pressure and its role in cell function
• Centrifugation and its applications in biological research

VIII. Ionizing Radiation and its Interaction with Matter (2 weeks)

• Types of ionizing radiation (alpha particles, beta particles, gamma rays)
• Interaction of radiation with matter (photoelectric effect, Compton scattering, pair production)
• Biological effects of ionizing radiation

IX. Applications of Ionizing Radiation in Medicine (1 week)

• Production of radioisotopes for medical imaging and therapy
• Nuclear medicine techniques (e.g., PET scan, radiation therapy)

X. Course Review and Summary (1 week)

• Review of key concepts covered in the course
• Applications of biophysics in various fields

Additional Resources:

• Here are some recommended textbooks for the course outlined above:
• Biological Physics by Philip Nelson (This is a great introductory text that covers a wide range of topics in biophysics, from thermodynamics and statistical mechanics to molecular motors and cellular signaling.)
• Physical Biology of the Cell by Rob Phillips, Jane Kondev, Julie Theriot, and Herman Garcia (This more advanced text delves deeper into the physical principles underlying cellular processes.)
• Biophysics: Searching for Principles by Bill Bialek (This graduate-level text offers a unique perspective on biophysics, focusing on the fundamental principles that govern biological systems.)
• The best textbook for you will depend on your background and level of interest in biophysics. If you are a beginner, then Biological Physics by Philip Nelson is a great place to start. If you have a strong foundation in physics and biology, then you may prefer Physical Biology of the Cell by Rob Phillips or Biophysics: Searching for Principles by Bill Bialek.
• In addition to the textbooks listed above, there are many other excellent resources available for learning about biophysics. These include online lectures, scientific articles, and popular science books.
• Online resources (e.g., Khan Academy lectures on biophysics)

Lecture I: Definition and Scope of Biophysics

Introduction to Biophysics

Biophysics is an interdisciplinary science that merges the principles and methods of physics with the complexities of biology. The primary goal of biophysics is to understand the fundamental processes that underlie living systems by applying the rigorous quantitative methods characteristic of physics.

• Key Aspects of Biophysics

1. Understanding the Structure and Function of Biomolecules

Molecular Structure:  Biophysics examines how biomolecules such as proteins and nucleic acids are structured.

Molecular Dynamics: Using thermodynamics and mechanics, biophysicists study how these molecules fold, interact with each other, and perform their specific functions within the cell.

2. Investigating the Physical Properties of Cells and Tissues

Cell Mechanics: Forces and pressures within and on cells are critical to their function and biophysics explores these mechanical properties.

Membrane Transport: The movement of substances across cell membranes and the role of physical forces in these processes are key areas of study.

Electrical Signals: The generation and transmission of nerve impulses are examined through the lens of biophysical principles.

3. Developing and Utilizing Biophysical Techniques

X-ray Crystallography: Used to determine the atomic structure of biomolecules.

Spectroscopy: Employed to study the interactions and dynamics of biomolecules.

Microscopy: Various forms, including electron and fluorescence microscopy, are crucial for visualizing cells and molecular interactions.

• The Scope of Biophysics

Biophysics encompasses a broad range of topics, each contributing to a deeper understanding of biological systems. The main areas include:

1. Molecular Biophysics

• Focuses on understanding the detailed structure and function of biomolecules.
• Studies how biomolecular interactions underpin cellular functions.

2. Cellular Biophysics

• Investigates the physical principles governing cellular processes.
• Includes the study of cytoskeletal dynamics, intracellular transport, and cellular signaling.

3. Membrane Biophysics

• Examines the properties of biological membranes.
• Investigates membrane dynamics, transport mechanisms, and signal transduction.

4. Neuroscience Biophysics

• Explores the biophysical mechanisms underlying nerve function and brain activity.
• Studies the electrical properties of neurons and the biophysics of synaptic transmission.

5. Medical Biophysics

• Applies biophysical principles to medical science.
• Develops diagnostic tools and therapeutic strategies based on biophysical research.
• Contributes to understanding diseases at a molecular and cellular level.

Conclusion

Biophysics plays a vital role in bridging physics and biology, providing profound insights into the mechanics of life. By integrating these disciplines, biophysics advances our understanding of biological systems, contributing significantly to fields such as medicine, drug discovery, biotechnology, and bioengineering. This interdisciplinary approach not only enhances our knowledge of living organisms but also drives innovation in technology and therapeutic practices.

Lecture II: Importance of Biophysics in Biological Sciences and Medicine

Introduction

Biophysics is pivotal in advancing both biological sciences and medicine. By applying the principles and techniques of physics, biophysics provides a deeper understanding of biological systems and contributes to the development of medical innovations. This interdisciplinary approach is essential for addressing complex biological questions and improving healthcare outcomes.

I.  Importance of Biophysics in Biological Sciences

1. Understanding Biological Processes

Molecular Mechanisms: Biophysics helps unravel the detailed mechanisms of molecular interactions, including protein folding, enzyme function, and DNA replication.

Molecular mechanisms refer to the specific biochemical processes that occur within living cells, governing the interactions between biomolecules such as proteins, nucleic acids, lipids, and carbohydrates. Understanding these mechanisms is crucial for deciphering the intricate web of life at the molecular level. Biophysics plays a pivotal role in this by applying physical principles and techniques to study and elucidate these processes.

• Protein Folding

Definition: Protein folding is the process by which a polypeptide chain folds into its three-dimensional, functional structure.

Significance: Proper folding is essential for protein functionality, as the structure determines the protein’s ability to interact with other molecules and perform its biological roles.

• Biophysical Techniques and Principles in protein folding

1. Thermodynamics:

Free Energy Landscapes: Biophysics uses concepts of free energy to understand the stability of protein conformations. Proteins fold into the lowest free energy state, and biophysicists study these landscapes to predict folding pathways and intermediates.

Stability Analysis: Techniques like differential scanning calorimetry (DSC) and isothermal titration calorimetry (ITC) measure the stability of proteins by analyzing their thermal properties and binding interactions.

1. Kinetics:

Folding Rates: Biophysical methods such as stopped-flow spectroscopy and circular dichroism (CD) spectroscopy help determine the rates at which proteins fold and unfold, providing insights into the kinetic barriers and intermediates.

1. Structural Studies:

  X-ray Crystallography: Provides high-resolution structures of folded proteins, allowing detailed visualization of atomic arrangements.

 Nuclear Magnetic Resonance (NMR) Spectroscopy: Offers information on protein dynamics and structures in solution, capturing transient states during folding.

 Cryo-Electron Microscopy (Cryo-EM): Enables visualization of large protein complexes and dynamic structures at near-atomic resolution.

• Enzyme Function

Definition: Enzymes are biological catalysts that accelerate chemical reactions in the cell. Understanding enzyme function involves studying how they bind substrates, catalyze reactions, and release products.

Significance: Enzymes are central to metabolism, signaling, and other cellular processes, and their dysfunction can lead to diseases.

• Biophysical Techniques and Principles

1. Kinetics:

Michaelis-Menten Kinetics: Biophysics applies kinetic models to describe the rate of enzyme-catalyzed reactions. Techniques like stopped-flow and rapid quench-flow methods measure reaction rates and transient intermediates.

1. Mechanistic Studies:

Single-Molecule Techniques: Methods like single-molecule fluorescence resonance energy transfer (smFRET) and atomic force microscopy (AFM) track the behavior of individual enzyme molecules, revealing details about their catalytic cycles and conformational changes.

1. Structural Studies:

X-ray Crystallography and Cryo-EM: Provide detailed structures of enzyme-substrate complexes, revealing active site geometry and mechanisms of catalysis.

NMR Spectroscopy: Offers insights into enzyme dynamics and interactions in solution, capturing conformational changes during catalysis.

1. Thermodynamics:

Binding Studies: Techniques such as ITC and surface plasmon resonance (SPR) measure the thermodynamics of substrate binding, providing information on binding affinities and interaction energies.

• DNA Replication

Definition: DNA replication is the process by which a cell duplicates its genetic material before cell division. This involves unwinding the double helix, synthesizing new strands, and ensuring accuracy.

Significance: Accurate DNA replication is crucial for maintaining genetic integrity across generations. Errors in replication can lead to mutations and diseases, including cancer.

• Biophysical Techniques and Principles

1. Structural Studies:

 X-ray Crystallography: Provides detailed structures of replication proteins and complexes, such as DNA polymerase and the replication fork, revealing how these proteins interact with DNA.

Cryo-EM: Allows visualization of large replication complexes and their dynamic assembly and disassembly during the replication process.

1. Kinetics and Dynamics:

Single-Molecule Techniques: Single-molecule fluorescence and optical tweezers track the real-time activity of replication proteins on individual DNA molecules, providing insights into the dynamics and coordination of replication.

FRET and Atomic Force Microscopy: Measure conformational changes and interactions between replication proteins and DNA.

1. Mechanistic Studies:

Enzyme Function: Studies on DNA polymerase kinetics and fidelity, including how it incorporates nucleotides and corrects errors, are conducted using stopped-flow and rapid quench-flow techniques.

1. Thermodynamics:

Binding Studies: ITC and SPR are used to study the binding thermodynamics of replication proteins to DNA, revealing the energetics of replication initiation and elongation.

Conclusion

Biophysics provides a comprehensive toolkit for dissecting the molecular mechanisms underlying protein folding, enzyme function, and DNA replication. By integrating structural, kinetic, and thermodynamic analyses, biophysics not only enhances our understanding of these fundamental biological processes but also informs the development of new therapeutic strategies and technologies. This detailed understanding is crucial for advancing both basic biological research and applied medical sciences.

II. Cellular Dynamics in Biophysics

Cellular Dynamics: It offers insights into cellular processes such as signal transduction, cell division, and motility, which are critical for understanding life at the cellular level.

Cellular dynamics refers to the study of the various processes and activities within a cell that are crucial for its function and survival. Biophysics plays a key role in understanding these processes by applying physical principles and advanced techniques.

Key Processes

1. Signal Transduction

Definition: The process by which cells respond to external signals through a series of molecular events, leading to a cellular response.

Importance: Essential for communication between cells and the regulation of cellular activities.

Biophysical Insights: Techniques like fluorescence resonance energy transfer (FRET) and live-cell imaging track the movement and interaction of signaling molecules in real-time.

2. Cell Division

Definition: The process by which a single cell divides into two daughter cells, ensuring the proper distribution of genetic material.

Importance: Fundamental for growth, development, and tissue repair.

Biophysical Insights: Microscopy techniques, such as time-lapse fluorescence microscopy, allow visualization of chromosome movement and spindle dynamics during mitosis.

3. Cell Motility

 Definition: The ability of cells to move and navigate their environment.

 Importance: Critical for processes like wound healing, immune responses, and development.

 Biophysical Insights: Methods like atomic force microscopy (AFM) and traction force microscopy measure the forces exerted by and on cells during movement, providing insights into the mechanics of cell motility.

Conclusion

Biophysics provides essential tools and methods for investigating cellular dynamics, offering deep insights into signal transduction, cell division, and motility. These insights are critical for understanding the fundamental processes that sustain life at the cellular level.

III. Technological Advancements in Biophysics

Imaging Techniques

Development of advanced imaging methods like cryo-electron microscopy and super-resolution microscopy allows for high-resolution visualization of cellular and molecular structures.

1. Cryo-Electron Microscopy (Cryo-EM)

Description: Cryo-EM is a method where samples are rapidly frozen, preserving their native structure without the need for staining or fixing.

 Resolution: Provides near-atomic resolution images of biomolecules and cellular structures.

 Applications: Used to visualize the architecture of complex biological macromolecules, such as viruses, ribosomes, and protein complexes. It has revolutionized structural biology by allowing scientists to observe molecules in their functional state.

2. Super-Resolution Microscopy

Description: A group of techniques that surpass the diffraction limit of traditional light microscopy, achieving much higher resolution.

 Types:  Includes methods like STED (Stimulated Emission Depletion) microscopy, PALM (Photoactivated Localization Microscopy), and STORM (Stochastic Optical Reconstruction Microscopy).

Applications: Enables detailed imaging of sub-cellular structures, such as protein distributions and interactions within live cells, down to the nanometer scale.

Analytical Tools

Biophysical techniques such as spectroscopy, atomic force microscopy, and X-ray crystallography enable precise analysis of biomolecular properties and interactions.

1. Spectroscopy

Types and Uses:

Nuclear Magnetic Resonance (NMR) Spectroscopy: Used to determine the structure and dynamics of proteins and nucleic acids in solution. Provides information on molecular interactions and conformational changes.

Fluorescence Spectroscopy: Used to study the dynamics of biological molecules, including protein folding and conformational changes, by tracking fluorescently labeled molecules.

Mass Spectrometry: Used to analyze the mass and composition of biomolecules, helping in identifying proteins, nucleic acids, and metabolites.

Applications: Allows for precise analysis of molecular properties and interactions, essential for understanding biochemical pathways and mechanisms.

2. Atomic Force Microscopy (AFM)

Description: A type of scanning probe microscopy that provides topographical imaging at the nanometer scale by scanning a sharp tip over the sample surface.

Capabilities: Measures forces between the tip and the sample, providing information on mechanical properties and interactions at the molecular level.

Applications: Used to study the surface structure of cells, proteins, and other biomolecules, as well as their mechanical properties.

3. X-ray Crystallography

Description: A technique that determines the atomic structure of crystalline biomolecules by measuring the diffraction patterns of X-rays passing through the crystal.

Resolution: Provides atomic-level resolution of molecular structures.

Applications: Critical for understanding the three-dimensional structures of proteins, nucleic acids, and complexes, aiding in the elucidation of their functions and mechanisms. It is widely used in drug design to visualize the binding sites of target molecules.

Conclusion

Technological advancements in biophysics, including cutting-edge imaging techniques and precise analytical tools, have dramatically enhanced our ability to visualize and analyze biological structures and processes at molecular and cellular levels. These advancements facilitate a deeper understanding of complex biological systems, driving progress in both basic research and applied medical sciences.

IV. Interdisciplinary Research

Bridging Disciplines: Biophysics integrates knowledge from physics, chemistry, biology, and computational science, fostering interdisciplinary collaboration and innovation.

Quantitative Approaches: It introduces quantitative methods to biology, enhancing the precision and reproducibility of biological research.

V. Importance of Biophysics in Medicine

1. Diagnostic Innovations

Medical Imaging: Techniques such as MRI, CT scans, and PET scans, rooted in biophysics, are indispensable for non-invasive diagnosis and monitoring of diseases.

Molecular Diagnostics:  Biophysical methods contribute to the development of diagnostic assays that detect biomarkers for various diseases, enabling early diagnosis and personalized medicine.

2. Therapeutic Developments

Drug Discovery: Biophysical approaches are crucial in drug design and screening, helping to identify and optimize therapeutic compounds.

Targeted Therapies: Understanding the biophysics of disease mechanisms allows for the development of targeted therapies that are more effective and have fewer side effects.

3. Understanding Disease Mechanisms

Pathophysiology: Biophysics provides insights into the molecular and cellular basis of diseases, including cancer, neurodegenerative disorders, and cardiovascular diseases.

Biomolecular Interactions: Studying the interactions between pathogens (e.g., viruses, bacteria) and host cells informs the development of vaccines and antiviral therapies.

4. Innovation in Treatment Techniques

 Radiation Therapy: Principles of physics are applied to optimize radiation doses for cancer treatment, minimizing damage to healthy tissues.

Bioengineering: Biophysics contributes to the design of medical devices, prosthetics, and tissue engineering, improving patient care and quality of life.

Conclusion

Biophysics is a cornerstone of modern biological sciences and medicine, offering essential tools and insights for understanding and manipulating biological systems. Its contributions to diagnostics, therapeutics, and medical technologies are vital for advancing healthcare and improving patient outcomes. By continuing to integrate physics with biology, biophysics drives innovation and fosters a deeper comprehension of life and disease, paving the way for future scientific and medical breakthroughs.

VI.  Questions and Solutions

Question 1: How does cryo-electron microscopy (Cryo-EM) differ from traditional electron microscopy, and what are its key advantages in studying biomolecules?

Solution:

Cryo-electron microscopy (Cryo-EM) involves rapidly freezing biological samples to preserve their native structure without the need for staining or fixing, unlike traditional electron microscopy which often requires staining. Key advantages of Cryo-EM include:

Near-Atomic Resolution: Allows visualization of biomolecules at near-atomic resolution, capturing fine structural details.

Preservation of Native State: Samples are studied in a state that closely resembles their natural environment, providing more accurate structural data.

Versatility: Suitable for a wide range of biological specimens, from small proteins to large complexes like viruses and ribosomes.

Question 2: What are the key features and applications of super-resolution microscopy in cellular biology?

Solution:

Super-resolution microscopy surpasses the diffraction limit of traditional light microscopy, achieving much higher resolution. Key features include:

Types of Techniques: Includes STED (Stimulated Emission Depletion) microscopy, PALM (Photoactivated Localization Microscopy), and STORM (Stochastic Optical Reconstruction Microscopy).

High Resolution: Provides nanometer-scale resolution, enabling detailed imaging of sub-cellular structures.

Applications: Used to study protein distributions, interactions, and dynamics within live cells, revealing details that are not visible with conventional microscopy.

Question 3: Describe the role of spectroscopy in biophysics and give examples of its different types and their applications.

Solution:

Spectroscopy in biophysics is used to analyze the properties and interactions of biomolecules. Examples include:

Nuclear Magnetic Resonance (NMR) Spectroscopy: Determines the structure and dynamics of proteins and nucleic acids in solution. Used to study molecular interactions and conformational changes.

Fluorescence Spectroscopy: Tracks fluorescently labeled molecules to study dynamics such as protein folding and conformational changes.

Mass Spectrometry: Analyzes the mass and composition of biomolecules, aiding in the identification of proteins, nucleic acids, and metabolites.

Question 4: What insights does atomic force microscopy (AFM) provide in the study of biomolecules, and what are its key applications?

Solution:

Atomic force microscopy (AFM) provides topographical imaging at the nanometer scale by scanning a sharp tip over the sample surface. Key insights and applications include:

Surface Structure: Reveals the surface structure of cells, proteins, and other biomolecules.

Mechanical Properties: Measures forces between the tip and the sample, providing information on molecular interactions and mechanical properties.

Applications: Used to study the detailed surface features and mechanical behavior of biomolecules, important for understanding their function and interactions.

Question 5: Explain the importance of X-ray crystallography in biophysics and its role in drug design.

Solution:

X-ray crystallography is crucial in biophysics for determining the atomic structure of crystalline biomolecules. Its importance and role in drug design include:

High Resolution: Provides atomic-level resolution of molecular structures.

Structural Understanding: Essential for understanding the three-dimensional structure of proteins, nucleic acids, and complexes.

Drug Design: Helps visualize the binding sites of target molecules, aiding in the design of drugs by revealing how they interact with their targets at the molecular level. This structural information is critical for optimizing the efficacy and specificity of therapeutic compounds.

Lecture III. Thermodynamic Principles in Biology

Thermodynamics is a branch of physics that deals with the relationships between heat, work, temperature, and energy. It provides a framework for understanding how energy flows and transforms within a system. In biology, thermodynamics plays a crucial role in explaining various cellular processes and maintaining the delicate balance within living organisms.

• Laws of Thermodynamics

There are four fundamental laws of thermodynamics that govern energy transfer and transformations:

1. Zeroth Law of Thermodynamics:

The Zeroth Law of Thermodynamics is foundational in the study of thermodynamics because it defines the concept of temperature and thermal equilibrium. Here’s a more detailed breakdown:

Statement of the Law

The Zeroth Law of Thermodynamics states:

If two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.

Mathematical Representation

This can be mathematically expressed as:

If ( T_A = T_B) and ( T_B = T_C ), then \( T_A = T_C).

Here:

( T_A ) is the temperature of system A.

( T_B) is the temperature of system B.

( T_C ) is the temperature of system C.

Explanation and Implications

1. Thermal Equilibrium: When two systems are in thermal equilibrium, they are at the same temperature, and no heat flows between them. This means their thermal states are stable and balanced.

Implication: If system A is in thermal equilibrium with system B, and system B is in thermal equilibrium with system C, then systems A and C must also be in thermal equilibrium with each other. This implies that all three systems share the same temperature.

The Zeroth Law allows the definition of temperature as a measurable quantity. If we use a thermometer (system B) to measure the temperature of system A and system C, and the thermometer reads the same for both, we can conclude that systems A and C are at the same temperature.

2. First Law of Thermodynamics:

The total energy of an isolated system remains constant. This implies that energy can neither be created nor destroyed, only transformed from one form to another. Mathematically, this can be written as:

ΔE = Q + W

In this equation:

 ΔE is the change in internal energy of the system.

Q is the heat transferred into the system (positive) or out of the system (negative).

W is the work done by the system (positive) or on the system (negative).

3. Second Law of Thermodynamics:

The entropy of an isolated system always increases over time. Entropy is a measure of disorder or randomness within a system. This law suggests that all spontaneous processes proceed towards a state of higher entropy. Mathematically, the entropy change (ΔS) can be related to the heat transfer (Q) and temperature (T) as:

ΔS ≥ Q/T

4. Third Law of Thermodynamics:

The entropy of a system approaches a constant value as the temperature approaches absolute zero (0 K). This law implies that a system can never achieve absolute zero temperature.

These laws provide a foundation for understanding energy flow and transformations in biological systems.

Enthalpy, Entropy, and Free Energy

Enthalpy (H): Enthalpy represents the total energy of a system, including its internal energy and the pressure-volume work it can perform on the surroundings. The change in enthalpy (ΔH) during a process is the amount of heat transferred at constant pressure.

Entropy (S): 

Entropy is a measure of the disorder or randomness within a system. A higher entropy state signifies greater disorder.

Free Energy (G): 

Free energy (G) combines the concepts of enthalpy and entropy to determine the spontaneity of a process under constant pressure and temperature. It can be calculated using the following equation:

G = ΔH – TΔS

A negative value of ΔG indicates a spontaneous process, while a positive ΔG signifies a non-spontaneous process. Processes can also be at equilibrium when ΔG = 0.

These thermodynamic functions are crucial for analyzing various biological processes. For instance, enzyme kinetics explores how enzymes accelerate biochemical reactions by lowering the activation energy, thereby increasing the rate of the reaction and making it more favorable according to the principles of free energy.

• Applications of Thermodynamics in Biological Systems

Thermodynamics has numerous applications in understanding biological phenomena:

• Enzyme Kinetics:

As mentioned earlier, enzyme kinetics utilizes the concept of free energy to explain how enzymes enhance reaction rates. By lowering the activation energy, enzymes make reactions more favorable and thus occur at a faster pace.

• Membrane Transport:

The movement of molecules across cell membranes is another example where thermodynamics plays a role. The movement of substances often occurs from a region of lower concentration (higher chemical potential) to a region of higher concentration (lower chemical potential). This passive transport is driven by the system’s tendency to minimize free energy and reach equilibrium.

• Muscle Contraction: 

Muscle contraction involves the hydrolysis of ATP (adenosine triphosphate) to release energy. The change in free energy (ΔG) of ATP hydrolysis provides the energy required for muscle movement.

By understanding these thermodynamic principles, we gain valuable insights into the intricate energy balance and processes that occur within living organisms.

Lecture IV: Energy Transfer in Living Systems

Different Forms of Energy

Introduction to Energy in Biological Systems

Energy is a fundamental concept in biology, as it powers all biological processes. This means that without energy, living organisms would be unable to perform essential functions such as growth, reproduction, and maintenance of cellular structures. Energy is required for everything from the synthesis of complex molecules to the movement of muscles and the transmission of nerve impulses. In essence, energy is the driving force behind life itself, enabling organisms to maintain order, respond to their environment, and carry out the biochemical reactions necessary for survival.

The primary forms of energy relevant to living systems include kinetic, potential, and chemical energy.

1. Kinetic Energy

Kinetic Energy in Biological Systems

Kinetic energy refers to the energy an object possesses due to its motion. In the context of biological systems, this motion can occur at various scales, from the microscopic movements of individual molecules to the macroscopic movements of entire organisms.

Understanding Kinetic Energy:

Imagine a ball rolling down a hill. The faster the ball rolls, the more kinetic energy it has. The key factors influencing the kinetic energy of an object in motion are:

• Mass (m): Heavier objects generally have more kinetic energy when moving at the same speed as lighter objects.
• Velocity (v): The speed and direction of the object’s movement. Higher velocity translates to greater kinetic energy. The formula for kinetic energy (KE) reflects this relationship: KE = 1/2 * m * v^2 (one-half times mass multiplied by the square of velocity).

Biological Examples of Kinetic Energy:

1. Diffusion: Cellular processes rely heavily on diffusion, the movement of molecules from an area of high concentration to an area of low concentration. Each molecule undergoing diffusion possesses kinetic energy due to its random thermal motion. This kinetic energy allows molecules to overcome concentration gradients and reach equilibrium.
2. Muscle Contractions: Muscle contraction relies on the coordinated movement of protein filaments called actin and myosin. During contraction, these filaments slide past each other, generating the force needed for movement. The movement of these filaments represents kinetic energy at the cellular level, ultimately powering the macroscopic movement of muscles.
3. Brownian Motion: This random movement of microscopic particles suspended in a fluid is another example of kinetic energy. Even though the particles themselves might be very small, their continuous motion due to collisions with surrounding fluid molecules showcases the concept of kinetic energy at play.
4. Flagellar Movement: Some bacteria and single-celled organisms possess flagella, whip-like structures that propel them through their environment. The rotation of these flagella involves the movement of proteins and other cellular components, all contributing to the kinetic energy responsible for the organism’s movement.

By understanding the concept of kinetic energy, we gain a deeper appreciation for the dynamic nature of life processes. From the submicroscopic world of molecule interactions to the observable movements of organisms, kinetic energy plays a crucial role in how biological systems function.

2. Potential Energy

Potential energy is the stored energy an object possesses due to its position or configuration within a force field. Unlike kinetic energy associated with motion, potential energy represents a dormant form of energy waiting to be converted into another form, typically kinetic energy.

Understanding the Concept:

Imagine a stretched rubber band. The further you stretch it, the more potential energy it stores because of the increased tension within the material. Once released, this potential energy can be converted into kinetic energy as the rubber band snaps back to its original position.

Force Fields and Potential Energy:

• Gravity: The most common force field in biological systems is gravity. Water held in a dam at a high elevation possesses gravitational potential energy due to its position relative to the Earth’s surface. When released, the water flows down, converting its potential energy into kinetic energy that can be used to generate electricity through turbines.
• Chemical Bonds: Within biological molecules, atoms are linked by chemical bonds. These bonds store potential energy due to the arrangement of electrons between atoms. Breaking these bonds releases energy, which can be harnessed to power various cellular processes.

Examples in Biological Systems:

1. Chemical Bonds: The primary example in biology is the potential energy stored within the chemical bonds of molecules like glucose, fats, and proteins. These molecules serve as the main energy source for cells. When these bonds are broken down during cellular respiration (e.g., breaking glucose into simpler molecules), the released potential energy is captured and transferred to ATP, the cell’s energy currency.
2. Elastic Potential Energy: Muscles contain elastic proteins like actin and myosin. When these muscles are stretched, the proteins store potential energy due to the increased tension within the muscle fibers. This stored energy is then released during muscle contraction, converting into kinetic energy that allows for movement.
3. Membrane Transport: Movement of molecules across biological membranes often involves manipulating potential energy gradients. For example, the active transport of ions across membranes against concentration gradients requires energy input, often from ATP hydrolysis. This process utilizes the potential energy stored in ATP to overcome the energy barrier for movement.
4. Macromolecular Interactions: The specific binding of molecules like enzymes to substrates is crucial for biological function. The interaction between these molecules often involves a “lock-and-key” fit, where the initial attraction between the molecules stores potential energy. This potential energy can then be used to facilitate the chemical reaction catalyzed by the enzyme.

3. Chemical Energy

Chemical energy is a form of potential energy stored within the chemical bonds of molecules. This energy is a vital component of biological systems, providing the necessary power for various biochemical reactions and physiological processes.

Chemical Bonds and Energy Storage

• Chemical Bonds: Atoms in molecules are held together by chemical bonds, which include covalent bonds, ionic bonds, and hydrogen bonds. The energy stored in these bonds can be released when the bonds are broken during chemical reactions.
• Bond Energy: The amount of energy required to break a bond between two atoms is known as bond energy. Different types of bonds have different bond energies, reflecting the strength and stability of the bond.

Examples of Chemical Energy in Biological Molecules

• Glucose: A simple sugar that serves as a primary energy source for cells. The chemical energy in glucose is released during cellular respiration.

Glucose is like the fuel for the cellular engine. When consumed by cells, the chemical bonds within glucose are broken down during cellular respiration, releasing the stored energy. This released energy is then captured and transferred to ATP, the energy currency that powers various cellular processes. Think of glucose as the energy bar packed with potential, waiting to be broken down and used for cellular work.

ATP (Adenosine Triphosphate): The energy currency of the cell. ATP stores energy in its high-energy phosphate bonds, which can be quickly hydrolyzed to release energy for cellular activities.

ATP is like the cellular cash. While glucose holds a large amount of potential energy, it’s not directly usable by most cellular processes. ATP acts as an intermediary, capturing the energy released from breaking down glucose and other molecules. The energy stored in the phosphate bonds of ATP can then be readily transferred to power numerous cellular activities, making it the universal currency for cellular transactions.

Beyond Glucose and ATP

Numerous other molecules store chemical energy in biological systems.  Examples include:

• Fats (triglycerides) – store long-term energy reserves.
• Proteins – contain peptide bonds that can be broken down for energy.
• Nucleic acids (DNA and RNA) – store the genetic code and also contain usable chemical energy.

While glucose and ATP are central players in cellular energy transfer, other molecules also contribute to the biological energy landscape. Fats provide a high-density energy storage solution for long-term needs. Proteins can be broken down for energy when necessary. Even the molecules that carry our genetic code, DNA and RNA, hold usable chemical energy within their bonds. The diversity of energy-rich molecules showcases the intricate mechanisms employed by living organisms to store and utilize energy efficiently.

Energy Release and Utilization

• Cellular Respiration: The process by which cells convert chemical energy from nutrients (like glucose) into ATP, releasing energy for cellular functions.
  • Glycolysis: The breakdown of glucose into pyruvate, producing a small amount of ATP and NADH.
  • Citric Acid Cycle: Completes the breakdown of glucose by oxidizing acetyl-CoA to CO2, generating ATP, NADH, and FADH2.
  • Oxidative Phosphorylation: Uses the electron transport chain and chemiosmosis to produce the majority of ATP in cellular respiration.
• Photosynthesis: Plants capture light energy and convert it into chemical energy stored in glucose. This process involves the synthesis of ATP and NADPH in the light reactions, which are then used in the Calvin cycle to fix carbon into glucose.

Importance of Chemical Energy in Biological Systems

• Metabolism: Chemical energy drives metabolic pathways that synthesize and degrade biomolecules, ensuring the maintenance of cellular structure and function.
• Growth and Reproduction: Energy from chemical bonds powers the synthesis of DNA, RNA, and proteins, essential for cell division and organismal growth.
• Homeostasis: Maintaining stable internal conditions requires continuous energy input, which is provided by the controlled release of chemical energy from nutrients.
• Movement and Transport: Muscle contractions, active transport across cell membranes, and intracellular transport of organelles rely on the energy released from ATP.

Chemical energy is the lifeblood of biological systems. From the breakdown of glucose to the transfer of energy by ATP, chemical bonds play a crucial role in powering all cellular processes. Understanding chemical energy is fundamental to appreciating the complexity and efficiency of life.

Chemical energy underpins the very essence of life. It fuels the growth, movement, and reproduction of all living organisms. By unraveling the secrets of chemical energy storage and transfer, we gain a deeper understanding of the intricate workings of the biological world.

Energy Transfer Mechanisms in Biological Systems

Living organisms are constantly in flux, utilizing energy to maintain their complex functions. This energy doesn’t stay put; it needs to be transferred efficiently within and between cells and throughout the entire organism. In this lecture, we will explore the three primary mechanisms of energy transfer: radiation, conduction, and convection. Understanding these mechanisms provides insights into how biological systems maintain their energy balance and support essential life processes.

• Energy transfer is essential for maintaining the functions of living organisms.
• Living organisms require a constant supply of energy to perform various tasks, from growth and repair to movement and reproduction.
• This energy doesn’t stay confined to one location; it needs to be transferred efficiently within cells, between cells, and throughout the entire organism.

Imagine a campfire. The burning wood releases energy in the form of heat. This heat doesn’t stay localized; it transfers to the surrounding air, creating a warm updraft. Similarly, in biological systems, energy obtained from food or sunlight needs to be transferred to where it’s needed to power various cellular processes. These transfers occur through three main mechanisms: radiation, conduction, and convection.

1. Radiation

• Definition: Radiation is the transfer of energy through electromagnetic waves without the need for a medium (i.e., it can occur in a vacuum).
• Biological Example: Photosynthesis
  • Process: Plants capture radiant energy from the sun through pigments like chlorophyll.
  • Impact: This energy is then converted into chemical energy stored in glucose, which is used by the plant and other organisms that consume the plant.
  • Significance: Radiation is essential for life on Earth, as it drives the process of photosynthesis, which is the foundation of most food webs.
• Other Examples: Infrared radiation from warm-blooded animals, UV radiation affecting skin cells.

2. Conduction

• Definition: Conduction is the transfer of energy through direct contact between molecules, allowing energy to move from a region of higher temperature to a region of lower temperature.
• Biological Example: Heat Transfer in Organisms
  • Process: Heat generated by metabolic processes in cells is conducted through tissues.
  • Impact: This ensures that enzymes and other proteins function optimally by maintaining the necessary temperature range.
  • Significance: Conduction is critical for temperature regulation in endothermic (warm-blooded) animals, helping to maintain homeostasis.
• Other Examples: Conduction in plant roots transferring heat from the soil to the plant, conduction between cells in tissues.

3. Convection

• Definition: Convection is the transfer of energy through the movement of fluids (liquids or gases), where warmer, less dense fluid rises and cooler, denser fluid sinks, creating a flow.
• Biological Example: Circulatory System
  • Process: Blood circulates through the body, distributing heat, nutrients, and oxygen while removing waste products.
  • Impact: This system ensures that all cells receive the substances they need to perform their functions and maintain energy balance.
  • Significance: Convection is essential for efficient nutrient and gas exchange, particularly in larger organisms where diffusion alone would be insufficient.
• Other Examples: Movement of air in the respiratory system, convection currents in large bodies of water affecting marine life.

Role of ATP in Cellular Energy Transfer

ATP (Adenosine Triphosphate)

• Definition: ATP is the primary energy currency of the cell, storing and providing energy for numerous cellular processes.
• Structure: ATP consists of an adenosine molecule bonded to three phosphate groups, with high-energy bonds between the phosphates.
• Function:
  • Energy Release: When ATP is hydrolyzed (broken down) into ADP (adenosine diphosphate) and an inorganic phosphate (Pi), energy is released.
  • Utilization: This energy is used to power various cellular activities, such as muscle contraction, active transport of molecules across cell membranes, and biosynthesis of macromolecules.
• Significance: ATP is crucial for energy transfer within cells, allowing for the efficient and rapid response to energy demands.

Quiz Questions and Solutions: Energy Transfer in Biological Systems

Question 1: Define the three primary mechanisms of energy transfer and provide a biological example for each.

Solution:

1. Radiation: The transfer of energy through electromagnetic waves without the need for a medium.

Example: Photosynthesis in plants, where radiant energy from the sun is captured by chlorophyll and converted into chemical energy.

2. Conduction: The transfer of energy through direct contact between molecules, moving from a region of higher temperature to a region of lower temperature.

 Example: Heat transfer in warm-blooded animals, where metabolic heat is conducted through tissues to maintain optimal enzyme function.

3. Convection: The transfer of energy through the movement of fluids, where warmer, less dense fluid rises and cooler, denser fluid sinks, creating a flow.

 Example: The circulatory system in animals, where blood circulates, distributing heat, nutrients, and oxygen throughout the body.

Question 2: Explain how ATP functions as an energy carrier in cells. Include a description of its structure and the process of energy release.

Solution:

Structure: ATP (Adenosine Triphosphate) consists of an adenosine molecule bonded to three phosphate groups. The bonds between the phosphate groups are high-energy bonds.

Function: ATP acts as the primary energy currency of the cell. It stores energy in its high-energy phosphate bonds.

Energy Release: When ATP is hydrolyzed into ADP (Adenosine Diphosphate) and an inorganic phosphate (Pi), energy is released. This energy is then used to power various cellular activities such as muscle contraction, active transport across cell membranes, and biosynthesis of macromolecules.

Question 3: Describe how convection is used in the human circulatory system to maintain energy balance and support essential life processes.

Solution:

Process: The human circulatory system uses convection to circulate blood throughout the body. Blood, a fluid, moves continuously, distributing heat, nutrients, and oxygen to cells and tissues while removing waste products.

Impact: This ensures that all cells receive the necessary substances to perform their functions, helping to maintain energy balance and support essential life processes.

Significance: Convection in the circulatory system is critical for efficient nutrient and gas exchange, which is particularly important in larger organisms where diffusion alone would be insufficient.

Question 4: How does conduction differ from convection in terms of energy transfer mechanisms? Provide an example of each in a biological context.

Solution:

Conduction:

 Mechanism: Transfer of energy through direct contact between molecules, moving from a region of higher temperature to a region of lower temperature.

 Example: Heat transfer in warm-blooded animals, where metabolic heat is conducted through tissues to maintain optimal enzyme function.

 Convection:

 Mechanism: Transfer of energy through the movement of fluids, where warmer, less dense fluid rises and cooler, denser fluid sinks, creating a flow.

Example: The circulatory system in animals, where blood circulates, distributing heat, nutrients, and oxygen throughout the body.

Question 5: Why is the understanding of radiation important in the study of biological energy transfer? Use photosynthesis as an example to illustrate your answer.

Solution:

Importance: Understanding radiation is important because it is a primary mechanism by which energy from the sun is transferred to living organisms. This energy is essential for life on Earth, particularly through the process of photosynthesis.

Photosynthesis Example:

Process: In photosynthesis, plants capture radiant energy from the sun using pigments like chlorophyll. This energy is then converted into chemical energy stored in glucose.

Impact: The glucose produced during photosynthesis serves as an energy source for the plant and for other organisms that consume the plant.

Significance: Radiation drives the process of photosynthesis, which is the foundation of most food webs and a critical component of the Earth’s energy balance.

Lecture V: Bioelectricity (Ion Channels and Their Properties)

Introduction to Bioelectricity

Bioelectricity refers to the electrical processes that occur within living organisms, particularly the generation and transmission of electrical signals in nerve and muscle cells. These electrical signals are essential for various physiological functions, including communication between cells, regulation of heartbeat, muscle contraction, and many other vital processes. The study of bioelectricity encompasses understanding how electrical signals are generated, how they propagate through cells and tissues, and how they are used to coordinate complex biological activities.

Ion Channels and Their Properties

Definition:

Ion channels are specialized proteins embedded within the cell membrane. They act as microscopic gates, allowing specific charged particles, called ions (like sodium, potassium, calcium, and chloride), to flow across the membrane. This controlled movement of ions is crucial for the cell’s electrical activity, impacting various functions like nerve impulses, muscle contraction, and secretion.

Types of Ion Channels:

There are three main types of ion channels classified based on their opening and closing mechanisms:

1. Voltage-gated Ion Channels:
   • These channels respond to changes in the electrical voltage across the cell membrane (membrane potential).
   • When the membrane potential reaches a specific threshold, the channel opens or closes, allowing a specific ion flow.
   • This plays a vital role in generating action potentials, the electrical signals that travel along nerve cells.

(Imagine a dam controlled by water pressure. Voltage-gated channels are like gates that open or close depending on the water pressure pushing against them – the membrane potential – allowing specific water flow – the ion flow.)

2. Ligand-gated Ion Channels:
   • These channels are activated by the binding of specific molecules, called ligands, to a receptor site on the channel protein.
   • Ligands can be neurotransmitters, hormones, or other signaling molecules.
   • Binding of the ligand triggers a conformational change in the channel, opening or closing it for specific ions.

(Think of a key unlocking a door. Ligand-gated channels are like doors with specific keyholes. Only the correct ligand “key” can unlock the channel and allow ion passage.)

3. Mechanically-gated Ion Channels:
   • These channels respond to physical forces applied to the cell membrane, such as pressure, touch, or sound.
   • Mechanical deformation of the membrane triggers the opening or closing of the channel for specific ions.

(Imagine a pressure pad triggering a light switch. Mechanically-gated channels are like switches activated by pressure on the cell membrane, allowing ion flow.)

Properties of Ion Channels:

1. Selectivity: Ion channels are selective for specific ions. This selectivity is achieved through the channel’s size, shape, and charge distribution within the pore. Only ions with compatible properties can pass through efficiently.
2. Conductance: This property measures how easily ions flow through an open channel. It is influenced by factors like the channel’s diameter and the ion’s size and charge. Higher conductance allows for a greater flow of ions.
3. Gating: The mechanisms that control the opening and closing of ion channels are collectively termed gating. These mechanisms involve specific voltage changes, ligand binding, or mechanical forces, as described for the different channel types.

Function:

Ion channels play a critical role in generating and propagating electrical signals in excitable cells, primarily neurons and muscle cells. The controlled flow of ions across the membrane creates changes in voltage that can trigger action potentials. These action potentials act as electrical impulses that travel along nerve fibers or initiate muscle contractions. Additionally, ion channels are involved in various other cellular processes, including secretion, cell volume regulation, and sensory perception.

Illustrations:

Here’s a simplified illustration of an ion channel:

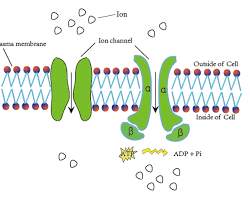
• The protein structure forms the channel pore.
• Selective filter allows only specific ions to pass.
• Gating mechanism (not shown here) controls channel opening/closing.

Understanding ion channels and their properties is essential for comprehending various physiological processes. They are also crucial targets for many drugs that act by modulating their function, impacting our nervous, muscular, and other systems.

Action Potentials and Nerve Impulse Transmission

Action Potentials

Definition: Action potentials are rapid, self-propagating electrical changes that travel along the length of a neuron. These transient bursts of voltage activity are the foundation of nerve impulse transmission in the nervous system.

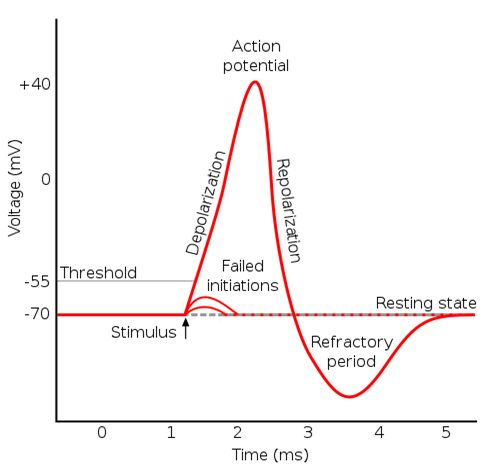
Phases of an Action Potential:

A single action potential can be broken down into five distinct phases, illustrated below:

Action potential phases diagram (https://teachmephysiology.com/nervous-system/synapses/action-potential/ )

1. Resting State: Neurons maintain a resting membrane potential, typically around -70 mV. This means the inside of the neuron is negatively charged compared to the outside. This potential is maintained by a higher concentration of potassium (K+) ions inside the cell and a higher concentration of sodium (Na+) ions outside. Leak channels allow for a small, constant flow of ions, but specific ion pumps (Na+/K+ ATPase) actively maintain the concentration gradients.
2. Depolarization: When a stimulus (neurotransmitter binding, sensory input) reaches a threshold level, voltage-gated Na+ channels open. This allows a rapid influx of Na+ ions into the cell, causing the membrane potential to become more positive (depolarize).
3. Repolarization: As the membrane potential reaches its peak (around +30 mV), voltage-gated K+ channels open. K+ ions then flow out of the cell, causing the membrane potential to return to its resting negative value (repolarize).
4. Hyperpolarization (Undershoot): In some cases, the K+ efflux can momentarily drive the membrane potential slightly more negative than the resting state. This brief period of hyperpolarization is followed by:
5. Return to Resting State: The Na+/K+ ATPase pump actively transports Na+ ions out of the cell and K+ ions back into the cell, restoring the original concentration gradients and returning the membrane potential to its resting state.

Equations:

The Nernst equation can be used to calculate the equilibrium potential (E) for an ion across a membrane, considering the concentration gradients and ion charge:

E = (RT / F) * ln ([X+]out / [X-]in)

where:

• R = Gas constant
• T = Absolute temperature
• F = Faraday’s constant
• [X+]out = Concentration of ion X outside the cell
• [X-]in = Concentration of ion X inside the cell

This equation helps explain the driving force for ion movement during the action potential. For example, at rest, the equilibrium potential for K+ is much more negative than the resting potential, favoring K+ efflux.

Nerve Impulse Transmission

Propagation of Action Potentials:

Action potentials travel along the axon of a neuron in an all-or-nothing manner. Once initiated, the depolarization at one point triggers the opening of voltage-gated Na+ channels in the adjacent membrane segment. This creates a new wave of depolarization that propagates down the axon.

Saltatory Conduction:

In myelinated axons, a fatty sheath insulates the axon except for periodic gaps called nodes of Ranvier. Action potentials only actively regenerate at these nodes, as the myelin sheath prevents ion flow along the internodal segments. This saltatory conduction (“jumping”) significantly increases the speed of action potential propagation compared to unmyelinated axons.

Synaptic Transmission:

The information carried by action potentials is ultimately transmitted between neurons at specialized junctions called synapses. There are two main types of synapses:

1. Electrical Synapses:

These synapses are less common and utilize gap junctions that allow direct electrical current flow between the presynaptic and postsynaptic neurons. This allows for very rapid transmission but limits the possibility for complex signal modulation.

2. Chemical Synapses:

These are the most common type of synapse. Here, the action potential in the presynaptic neuron triggers the release of neurotransmitters into the synaptic cleft. These neurotransmitters then bind to specific receptors on the postsynaptic neuron’s membrane, influencing its excitability. Depending on the type of neurotransmitter and receptor, this can either excite (increase the likelihood of an action potential) or inhibit (decrease the likelihood of an action potential) the postsynaptic neuron.

By understanding the generation and propagation of action potentials, as well as the different modes of synaptic transmission, we gain insight into the remarkable capabilities of the nervous system to process information and coordinate complex responses.

Electrical Properties of Cells

The electrical properties of cells are fundamental to their function, particularly in excitable cells like neurons and muscle cells. These properties arise from the controlled movement of charged particles called ions (e.g., sodium, potassium, calcium, chloride) across the cell membrane.

Membrane Potential

Definition: The membrane potential is the voltage difference between the interior and exterior of a cell membrane. This voltage difference arises due to the unequal distribution of ions across the membrane. Typically, there is a higher concentration of positively charged ions (cations) outside the cell and a higher concentration of negatively charged ions (anions) inside the cell.

This separation of charges creates an electrical field across the membrane, measurable as the membrane potential.

Importance: The membrane potential plays a critical role in the excitability of cells. In neurons and muscle cells, changes in the membrane potential can trigger action potentials, which are rapid electrical signals that propagate along the cell and are essential for communication and coordinated responses.

Illustration:

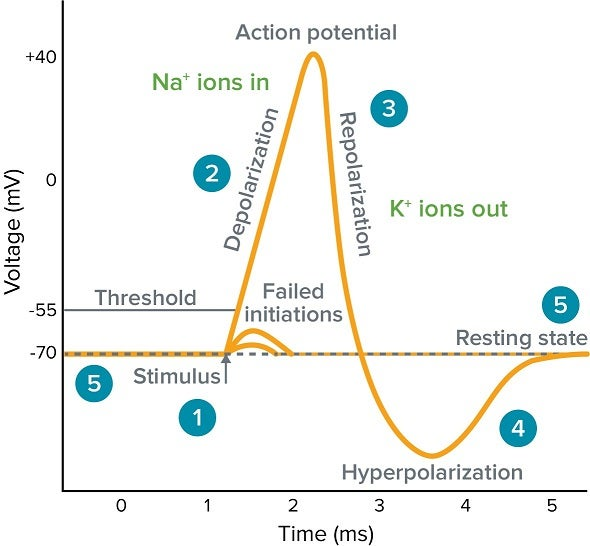
Membrane potential diagram (https://www.moleculardevices.com/applications/patch-clamp-electrophysiology/what-action-potential )

• The cell membrane separates the intracellular and extracellular spaces.
• Different ion concentrations are shown inside and outside the cell.
• The voltmeter measures the voltage difference (membrane potential).

Resting Potential

Definition: The resting potential is the stable voltage of a cell at rest. In neurons, the resting potential is typically around -70 millivolts (mV), meaning the inside of the cell is negative relative to the outside. This negative resting potential is crucial for maintaining cellular excitability.

Maintenance of Resting Potential:

Three main factors contribute to maintaining the resting potential:

1. Ion Gradients: There are unequal concentrations of ions across the cell membrane. For example, neurons have a higher concentration of potassium (K+) ions inside the cell and a higher concentration of sodium (Na+) ions outside. These concentration gradients create a driving force for ions to move across the membrane, influencing the resting potential.
2. Ion Pumps: Actively transport ions against their concentration gradients to maintain the imbalances. The most important ion pump in maintaining the resting potential is the sodium-potassium pump (Na+/K+ ATPase). This pump actively transports 3 Na+ ions out of the cell and 2 K+ ions into the cell, using energy derived from ATP hydrolysis. This pumping action counteracts the leak of ions through channels and helps maintain the K+ gradient, which is crucial for the resting potential.
3. Leak Channels: These are protein channels in the membrane that allow for a small, passive flow of ions down their concentration gradients. While leak channels contribute to the resting potential, the ion pumps work to maintain the gradients and prevent the complete equilibration of ions.

Equations:

The Nernst equation can be used to calculate the equilibrium potential (E) for an ion across a membrane, considering the concentration gradients and ion charge:

E = (RT / F) * ln ([X+]out / [X-]in)

where:

• R = Gas constant
• T = Absolute temperature
• F = Faraday’s constant
• [X+]out = Concentration of ion X outside the cell
• [X-]in = Concentration of ion X inside the cell

This equation helps explain the driving force for ion movement at rest. For example, at rest, the equilibrium potential for K+ is much more negative than the resting potential, favoring K+ efflux, which contributes to the negative resting potential.

By understanding the membrane potential and resting potential, we gain insights into how cells maintain a stable electrical state and prepare for the generation of action potentials, which are crucial for cellular communication and function.

Brief Introduction to Electrocardiogram (ECG) and Electroencephalogram (EEG)

These two techniques measure the electrical activity of different organs:

Electrocardiogram (ECG)

Definition: An ECG is a recording of the electrical activity of the heart muscle over time. It reflects the depolarization (excitation) and repolarization (recovery) of cardiac cells as they contract and relax during a heartbeat.

pen_spark

Purpose: ECG is a vital tool used by doctors to diagnose and monitor various heart conditions. It can help identify:

• Abnormal heart rhythms (arrhythmias)
• Heart attacks (myocardial infarction)
• Damage to the heart muscle
• Electrolyte imbalances
• Congenital heart defects

Components of an ECG:

The ECG waveform consists of distinct waves that represent specific electrical events in the heart cycle:

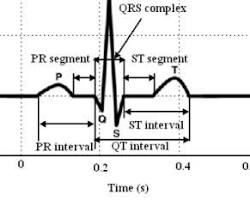
Opens in a new window www.researchgate.net

• P Wave: Represents the depolarization (electrical activation) of the atria, the upper chambers of the heart.
• QRS Complex: Corresponds to the ventricular depolarization, the rapid activation of the ventricles, the lower pumping chambers. This is the largest deflection on the ECG.
• T Wave: Reflects the repolarization of the ventricles, as they return to their resting state.
• U Wave (not always visible): Represents repolarization of specialized heart tissue.

By analyzing the shape, size, and timing of these waves, doctors can gain valuable insights into the heart’s function and identify potential abnormalities.

Electroencephalogram (EEG)

Definition: An EEG is a recording of the electrical activity of the brain, measured by electrodes placed on the scalp. It reflects the synchronized electrical activity of large populations of neurons in the brain.

Purpose: EEG is a valuable tool in diagnosing and monitoring various neurological conditions, including:

• Epilepsy: EEG can help identify abnormal brain activity patterns associated with seizures.
• Sleep disorders: EEG can be used to assess sleep stages and diagnose sleep disorders like sleep apnea.
• Brain tumors: EEG may show abnormal activity patterns associated with tumors.
• Coma: EEG can help assess the level of brain function in coma patients.

Types of Brain Waves:

EEG recordings show different patterns of electrical activity, categorized by their frequency:

• Delta Waves (0.5-4 Hz): Associated with deep sleep and unconsciousness.
• Theta Waves (4-8 Hz): Associated with light sleep, drowsiness, and daydreaming.
• Alpha Waves (8-13 Hz): Associated with relaxed wakefulness, eyes closed, and meditation.
• Beta Waves (13-30 Hz): Associated with active thinking, concentration, and alertness.

By analyzing the dominant frequency bands and patterns in the EEG, doctors can gain insights into brain function and identify potential abnormalities.

Key Differences:

Feature	ECG	EEG
Measured Organ	Heart	Brain
Electrical Activity	Cardiac muscle contraction	Neuronal activity
Purpose	Diagnose and monitor heart conditions	Diagnose and monitor neurological conditions
Recording Location	Chest	Scalp
Waveforms	P, QRS, T waves	Delta, Theta, Alpha, Beta waves
Frequency Range	Lower frequency (millihertz)	Higher frequency (hertz)

Questions and Solutions:

1. Action Potential Generation and Propagation:

Question: During an action potential, what factors determine whether a neuron will fire (generate an action potential)?

Solution: Whether a neuron fires depends on the strength of the stimulus it receives. A weak stimulus might only cause a small depolarization that doesn’t reach the threshold potential. However, a strong stimulus can cause a larger depolarization that crosses the threshold, triggering an action potential. The threshold potential is a specific voltage level at which the voltage-gated Na+ channels open rapidly, leading to a self-propagating action potential.

2. Ion Channels:

Question: How does the structure of an ion channel contribute to its selectivity for specific ions?

Solution: The selectivity of an ion channel is determined by a combination of factors:

• Size: The pore of the channel has a specific size that allows only ions of a certain size to pass through.
• Charge: The channel has fixed charges within its pore that attract or repel ions depending on their charge. Ions with a charge opposite to the channel’s lining can be attracted and pass through more easily.
• Hydration shell: Some ions, like sodium (Na+), have a strong attraction to water molecules. The channel’s structure might influence how easily these water molecules can accompany the ion through the pore, further affecting selectivity.

3. Resting Potential in Neurons:

Question: What would happen to a neuron’s ability to transmit signals if it couldn’t maintain its resting potential?

Solution: Maintaining the resting potential is crucial for a neuron’s ability to transmit signals. If the resting potential is disrupted, several issues could arise:

• Reduced excitability: Without a stable negative resting potential, neurons would be closer to their threshold potential. This could lead to spontaneous firing of action potentials, making it difficult to control signal transmission.
• Impaired signal propagation: Action potentials rely on the difference between resting and threshold potentials. If the resting potential is not maintained, the depolarization caused by the action potential might not be sufficient to reach the threshold at the next segment, hindering signal propagation.
• Energy depletion: Maintaining the resting potential requires the constant work of ion pumps. If the resting potential is lost, the neuron would need to expend even more energy to restore it, potentially impacting other cellular functions.

4. ECG vs. EEG:

Question: While both ECG and EEG measure electrical activity, how does the information they provide differ?

Solution: ECG and EEG provide information about different aspects of electrical activity:

• ECG: Measures the electrical activity of the heart muscle as it contracts and relaxes during a heartbeat. The ECG provides information about the heart rate, rhythm, and potential abnormalities in the conduction of electrical signals through the heart.
• EEG: Measures the synchronized electrical activity of large populations of neurons in the brain. The EEG provides information about brain function, including dominant brain wave frequencies associated with different states of consciousness (sleep, wakefulness, concentration). The EEG doesn’t directly measure individual neuron activity but reflects the overall electrical activity of brain regions.

Conclusion

Understanding bioelectricity is essential for comprehending how electrical signals are generated and transmitted in living organisms. By studying ion channels, action potentials, membrane potentials, and the applications of ECG and EEG, students will gain a deeper appreciation of the electrical nature of biological systems.

Lecture VI: Applications of Ultrasound in Biology and Medicine

Ultrasound is a versatile technology utilizing high-frequency sound waves that have numerous applications in biology and medicine. This section explores the principles behind ultrasound, its diverse medical uses, and the potential biological effects of ultrasound exposure.

Principles of Ultrasound Generation and Propagation

Generation:

Ultrasound waves are generated by piezoelectric crystals. These crystals vibrate when exposed to an electric current, producing sound waves at specific frequencies (typically above 20 kHz, beyond the range of human hearing). The frequency of the generated sound wave depends on the properties of the piezoelectric material and the applied voltage.

Propagation:

Once generated, ultrasound waves travel through a medium (e.g., tissue, water) at a characteristic speed. The speed of sound (c) in a medium depends on the density (ρ) and the bulk modulus (K) of the medium:

c = √(K / ρ)

The bulk modulus represents the material’s resistance to compression. Denser or stiffer materials generally have a higher speed of sound.

Properties of Ultrasound Waves:

• Frequency: As mentioned earlier, ultrasound waves have frequencies above the human hearing range (typically 20 kHz to several MHz).
• Wavelength: The wavelength (λ) is inversely proportional to the frequency (f) and the speed of sound (c):

λ = c / f

• Attenuation: As ultrasound travels through a medium, its intensity decreases due to absorption and scattering. Absorption is the conversion of sound energy into heat. Scattering occurs when the sound wave encounters boundaries or inhomogeneities in the medium, causing the wave to deflect in different directions.

Medical Applications of Ultrasound

Ultrasound has a wide range of applications in medicine, primarily due to its ability to:

• Create images of internal organs and tissues: Ultrasound imaging is a non-invasive and painless technique used for various diagnostic purposes.
• Deliver therapeutic effects: Ultrasound therapy uses targeted sound waves to promote healing, break down tissue, or induce specific cellular responses.

Imaging Applications:

• Prenatal care: Ultrasound imaging is a cornerstone of prenatal care, allowing visualization of the developing fetus, monitoring its growth, and detecting potential abnormalities.
• Abdominal imaging: Ultrasound can be used to examine abdominal organs like the liver, kidneys, and gallbladder for abnormalities.
• Pelvic imaging: Ultrasound can assess the uterus, ovaries, and other pelvic organs in women and the prostate gland in men.
• Echocardiography: This technique uses ultrasound to visualize the heart, assess its structure and function, and detect abnormalities in heart valves or chambers.
• Doppler ultrasound: This advanced technique measures blood flow within vessels using the Doppler effect, which can help diagnose blood clots or blockages.

Therapeutic Applications:

• Lithotripsy: Ultrasound therapy can be used to break down kidney stones or gallstones into smaller fragments that can be passed more easily.
• Physical therapy: Ultrasound therapy can promote healing in soft tissues, reduce pain and inflammation, and improve tissue repair.
• Cancer treatment: High-intensity focused ultrasound (HIFU) is a developing technique that uses targeted ultrasound waves to destroy cancer cells.

Bioeffects of Ultrasound

While generally safe, ultrasound exposure can have biological effects depending on the intensity, frequency, and duration of exposure. These effects can be thermal (heat generation) or non-thermal (mechanical effects on cells).

Thermal effects: High-intensity ultrasound can cause localized heating, which can be therapeutic in some applications but potentially damaging at higher intensities.

Non-thermal effects: Ultrasound can also exert mechanical forces on cells and tissues, potentially leading to:

• Cavitation: The formation and collapse of bubbles in the medium, which can damage cells.
• Microscopic displacements: Ultrasound waves can cause small-scale movements within cells, potentially affecting cellular processes.

Safety Considerations:

Medical ultrasound devices are designed and used to minimize potential bioeffects. The intensity and duration of exposure are carefully controlled to ensure safe diagnostic and therapeutic applications.

Solved Example:

A doctor uses ultrasound imaging with a frequency of 5 MHz to examine a patient’s kidney. The speed of sound in kidney tissue is approximately 1540 m/s. Calculate the wavelength of the ultrasound wave.

Solution:

λ = c / f = 1540 m/s / 5 MHz (convert MHz to Hz: 5 MHz * 10^6 Hz/MHz) = 0.308 mm

This example demonstrates how the wavelength of ultrasound can be calculated based on the frequency and speed of sound in the medium.

Further Exploration:

• Different types of ultrasound transducers and their functionalities.
• Contrast agents used in ultrasound imaging to enhance contrast between tissues.
• Emerging applications of ultrasound in drug delivery and gene therapy.

By understanding the principles, applications, and bioeffects

Principles of Ultrasound Generation and Propagation

Introduction to Ultrasound

Definition: Ultrasound refers to sound waves with frequencies higher than the upper audible limit of human hearing, typically above 20 kHz.

Applications: Used extensively in medical imaging (e.g., sonography), industrial non-destructive testing, and therapeutic procedures.

Principles of Ultrasound Generation

1. Piezoelectric Effect

Definition: The piezoelectric effect is the ability of certain materials to generate an electric charge in response to applied mechanical stress.

Materials: Common piezoelectric materials include quartz, Rochelle salt, and synthetic ceramics like lead zirconate titanate (PZT).

Generation of Ultrasound Waves

Transducer Function: Ultrasound waves are generated using a transducer that contains piezoelectric crystals.

Electrical Signal: An alternating current (AC) electrical signal is applied to the piezoelectric crystal.

Mechanical Vibration: The crystal vibrates in response to the AC signal, producing sound waves.

Frequency: The frequency of the ultrasound waves matches the frequency of the applied electrical signal.

Equation for Ultrasound Frequency

f=v/λ​

where:

• f is the frequency of the ultrasound wave,
• v is the speed of sound in the medium,
• λ is the wavelength of the sound wave.

Example:

If an ultrasound transducer generates waves at a frequency of 5 MHz (5 x 10^6 Hz) in soft tissue (speed of sound ≈ 1540 m/s), the wavelength is: λ= vf = 1540 m/s5×106 Hz=0.000308 m=0.308 mm

Principles of Ultrasound Propagation

2. Propagation of Sound Waves

Medium Requirement: Ultrasound waves require a medium (solid, liquid, or gas) to propagate.

Wave Types: Primarily longitudinal waves where particle displacement is parallel to wave propagation.

Understanding the Speed of Sound: Exploring the Equation v = √(K/ρ)

In the realm of physics, the speed of sound (v) is a fundamental property that dictates how fast sound waves travel through a particular medium. This vital concept is governed by a key equation:

v = √(K/ρ)

where:

• v represents the speed of sound (meters per second)
• K represents the bulk modulus of the medium (Pascals)
• ρ represents the density of the medium (kilograms per cubic meter)

This equation essentially expresses the speed of sound as the square root of the ratio between the bulk modulus (K) and the density (ρ) of the medium.

Breaking Down the Components:

• Bulk Modulus (K): This property reflects a material’s resistance to compression. A higher bulk modulus signifies a stiffer material that offers greater opposition to compressional forces.
• Density (ρ): This quantity refers to the mass per unit volume of a substance. Denser materials generally pack more particles into a given space, leading to a higher density.

The Relationship between K and ρ:

The equation reveals an inverse relationship between the speed of sound and the density of the medium. This means that sound travels faster in less dense materials (lower ρ) and slower in denser materials (higher ρ). Conversely, the bulk modulus (K) has a direct relationship with the speed of sound. A higher bulk modulus (stiffer material) translates to a faster speed of sound.

Real-World Examples:

Imagine sound waves propagating through air and water. Air, being less dense than water, has a lower bulk modulus. Consequently, the speed of sound in air is slower compared to water. This is why we hear sounds underwater seemingly “instantly” after they are produced, even though sound travels at a finite speed.

Beyond the Equation:

While the v = √(K/ρ) equation provides a fundamental understanding of sound speed, other factors can influence sound propagation in real-world scenarios. These factors include:

• Temperature: Generally, sound travels faster at higher temperatures due to increased molecular motion within the medium.
• Medium composition: The specific properties of the medium, beyond just bulk modulus and density, can also play a role.

3. Attenuation

The Fate of Sound Waves: Exploring Attenuation and the I = I₀e⁻αˣ Equation

As sound waves travel through a medium, their intensity, or strength, doesn’t remain constant forever. Various factors can weaken the sound wave over distance, reducing its perceived volume. This phenomenon is known as attenuation.

The Actors on the Attenuation Stage:

There are three primary culprits behind sound wave attenuation:

1. Absorption: This process involves the conversion of sound energy into another form of energy, typically heat. As sound waves travel through a medium, some of their energy gets absorbed by the medium’s particles, leading to a decrease in intensity.
2. Scattering: When sound waves encounter obstacles or inhomogeneities within the medium, they can deflect in various directions. This scattering effect can reduce the intensity of the original sound wave traveling in a specific direction. Imagine sound waves hitting a rough surface – they’ll bounce off in all directions, weakening the original sound traveling straight ahead.
3. Reflection: When sound waves reach a boundary between two media with different acoustic properties (sound propagation characteristics), a portion of the wave can be reflected back into the original medium. While reflection doesn’t necessarily reduce the overall sound energy, it can weaken the intensity of the transmitted sound wave that continues through the second medium.

The Equation Behind the Attenuation Story:

The equation I = I₀e⁻αˣ describes the relationship between the initial intensity (I₀) of a sound wave, the intensity (I) after traveling a distance (x), and the attenuation coefficient (α).

• I: Represents the intensity of the sound wave after traveling a distance x (units: watts per meter squared [W/m²]).
• I₀: Represents the initial intensity of the sound wave before traveling any distance (units: W/m²).
• α: Represents the attenuation coefficient (units: per meter [1/m]). This coefficient depends on the medium and frequency of the sound wave. Higher α values indicate greater attenuation over distance.
• x: Represents the distance traveled by the sound wave (units: meters [m]).
• e: Represents the mathematical constant Euler’s number (approximately 2.71828).

Understanding the Exponential Term:

The term e⁻αˣ in the equation is an exponential term that signifies the rapid decrease in intensity with increasing distance. As the distance (x) traveled by the sound wave increases, the exponent (αx) becomes larger, and the value of e⁻αˣ gets smaller very quickly. This translates to a significant drop in intensity (I) compared to the initial intensity (I₀).

Real-World Applications:

Understanding attenuation is crucial in various fields:

• Acoustics: Helps design buildings with optimal soundproofing or predict sound propagation in concert halls.
• Underwater acoustics: Explains the decrease in sound intensity with increasing water depth, impacting underwater communication and sonar effectiveness.
• Medical ultrasound: Accounts for the weakening of ultrasound waves as they travel through tissue, influencing image quality.

Example: Intensity Reduction in Ultrasound

Imagine an ultrasound wave with an initial intensity (I₀) of 100 watts per square meter (W/m²). The attenuation coefficient (α) is 0.1 per centimeter (cm⁻¹), and the wave travels through 5 centimeters (cm) of tissue. How much weaker (less intense) does the sound wave become (final intensity, I)?

We can use the following equation to calculate the final intensity:

I = I₀e⁻αx

where:

• I: Final intensity of the sound wave after traveling a distance (x) (units: W/m²)
• I₀: Initial intensity of the sound wave (units: W/m²)
• α: Attenuation coefficient (units: per centimeter, cm⁻¹)
• x: Distance traveled by the sound wave (units: centimeters, cm)
• e: Mathematical constant Euler’s number (approximately 2.71828)

Plugging in the values from our example:

I = 100 W/m² × e⁻⁰.¹ cm⁻¹ × 5 cm ≈ 60.65 W/m²

Using a calculator, we find that the final intensity (I) is approximately 60.65 W/m². This represents a decrease of about 39.35% in intensity compared to the initial value (I₀) due to attenuation during its travel through the tissue.

Explanation:

The term e⁻αˣ in the equation signifies a rapid decrease in intensity with increasing distance (x). As the distance traveled increases, the exponent (αx) becomes larger, and the value of e⁻αˣ gets smaller very quickly. This translates to a significant drop in intensity (I) compared to the initial intensity (I₀).

Unveiling the Mysteries of Ultrasound: Reflection, Refraction, Scattering, and Imaging

Ultrasound technology plays a vital role in medicine, utilizing high-frequency sound waves for diagnosis and therapeutic purposes. But how do these sound waves interact with different tissues, and how are they used to create images? This post delves into the fascinating world of ultrasound, exploring reflection, refraction, scattering, and the principles behind ultrasound imaging.

Beyond Attenuation: Reflection, Refraction, and Scattering

As sound waves travel through the body, they encounter boundaries between tissues with varying acoustic properties (resistance to sound propagation). These encounters can lead to three key phenomena:

1. Reflection: When a sound wave strikes a boundary between two dissimilar tissues, a portion of the wave bounces back into the original medium. This reflection is crucial for ultrasound imaging, as the reflected waves carry information about the tissues they encountered. The reflection coefficient determines the proportion of the incident intensity that gets reflected, calculated using the equation:

R = (Z₂ – Z₁ / Z₂ + Z₁)²

where:

• R: Reflection coefficient
• Z₁: Acoustic impedance of the first medium
• Z₂: Acoustic impedance of the second medium

2. Refraction: When a sound wave travels from one medium to another with a different sound speed, it changes direction at the boundary. This bending of the wave is known as refraction and is governed by Snell’s Law:

Sin θ₁ / sin θ₂ = v₁ / v₂

where:

• θ₁: Angle of incidence (angle the wave makes with the boundary in the first medium)
• θ₂: Angle of refraction (angle the wave makes with the boundary in the second medium)
• v₁: Speed of sound in the first medium
• v₂: Speed of sound in the second medium

Refraction can affect the path of sound waves within the body and influence image formation.

3. Scattering: Sound waves can also be scattered in various directions when they interact with small particles or inhomogeneities within a tissue. This scattering can reduce the intensity of the transmitted sound wave and contribute to image formation by providing information about tissue texture.

Example: Imagine ultrasound traveling from soft tissue (speed of sound = 1540 m/s) into bone (speed of sound = 4080 m/s). If the angle of incidence is 30°, what’s the angle of refraction?

Using Snell’s Law:

Sin θ₂ = sin 30° × 1540 / 4080 ≈ 0.125 θ₂ ≈ sin⁻¹(0.125) ≈ 7.2°

In this example, the sound wave bends significantly upon entering the denser bone.

Ultrasound Imaging: Making the Invisible Visible

By harnessing the principles of reflection and signal processing, ultrasound imaging creates visual representations of internal organs and tissues. Here are some key techniques:

1. A-mode (Amplitude Mode): This basic mode displays the amplitude (strength) of reflected sound waves as spikes on a time-based graph. The distance to a reflecting structure can be estimated based on the time it takes for the sound wave to travel and return.
2. B-mode (Brightness Mode): This widely used mode converts the amplitude information from reflected waves into a grayscale image. Tissue interfaces with strong echoes appear brighter, while weaker echoes appear darker. B-mode imaging provides detailed anatomical information.
3. Doppler Ultrasound: This technique analyzes the shift in frequency of reflected sound waves caused by moving structures like blood or tissue. This allows for the assessment of blood flow and tissue vibration.

Resolution and Penetration: Striking a Balance

The quality of ultrasound images depends on two crucial factors:

• Axial Resolution: The ability to distinguish between two closely spaced structures along the path of the ultrasound beam. Higher frequency sound waves provide better axial resolution but penetrate less deeply into the body.
• Lateral Resolution: The ability to distinguish between two structures side-by-side, perpendicular to the ultrasound beam. Similar to axial resolution, higher frequencies offer better lateral resolution.

There’s a trade-off between resolution and penetration. For visualizing superficial structures with high detail, a higher frequency transducer is chosen. Conversely, for examining deeper tissues, a lower frequency transducer with deeper penetration but lower resolution is preferred.

Summary                                                     

Understanding the principles of ultrasound generation and propagation involves:

– The piezoelectric effect and how transducers convert electrical signals into sound waves.

– The propagation of sound waves in different media, including attenuation and factors influencing wave behavior.

– The interactions of ultrasound waves with tissues, including reflection, refraction, and scattering, and their implications for imaging.

– The application of these principles in medical imaging, providing critical diagnostic information through various ultrasound modes.

Lecture VII: Fluid Flow and Viscosity in Biological Systems

Introduction to Fluid Flow and Viscosity

Fluids are essential components within living organisms. They include substances like blood, lymph, and respiratory gases, all playing vital roles in various physiological processes. But how do these fluids move and interact with their surroundings? This lecture delves into the fascinating world of fluid flow and viscosity in biological systems.

Fluid Flow in Biological Systems

Fluids, by definition, can flow and adapt to the shape of their containers. Understanding their properties, particularly viscosity, is crucial. Viscosity essentially reflects a fluid’s resistance to flow. Imagine honey versus water – honey has a higher viscosity, making it flow more slowly than water.

Properties of Fluids

Here are some key properties of fluids relevant to biological systems:

1. Viscosity (η): Measured in Pascal-seconds (Pa·s), viscosity indicates a fluid’s resistance to flow. A higher viscosity signifies greater resistance. The equation for dynamic viscosity is:

η = τ / (dv/dy)

where:

• τ (tau) is the shear stress (force per unit area exerted by the moving fluid).
• dv/dy represents the velocity gradient perpendicular to the flow direction (how rapidly the velocity changes across the fluid).
• Density (ρ): Density (measured in kilograms per cubic meter, kg/m³) refers to the mass per unit volume of a fluid. The equation for density is:

ρ = m / V

where:

• m is the mass of the fluid.
• V is the volume of the fluid.
• Shear Stress (τ): Shear stress (measured in Pascals, Pa) represents the force per unit area exerted by the fluid in motion. The equation for shear stress is:

τ = η * (dv/dy)

Example: Calculating Shear Stress in a Blood Vessel

Let’s imagine a blood vessel where the blood’s dynamic viscosity (η) is 3.5 mPa·s (millipascal-seconds) and the velocity gradient is 200 s⁻¹ (per second). How much shear stress (τ) is present?

τ = η * (dv/dy) = 3.5 × 10⁻³ Pa·s × 200 s⁻¹ ≈ 0.7 Pa

This calculation reveals a shear stress of approximately 0.7 Pa within the blood vessel.

Blood Flow and Its Regulation

Blood flow is a critical process for delivering oxygen and nutrients throughout the body. Here, we’ll explore its dynamics and regulation:

1. Blood Flow Dynamics:
2. Laminar Flow: This occurs in smaller blood vessels, where blood flows smoothly in distinct layers. Imagine layers of fluid sliding past each other like cards.
3. Turbulent Flow: This typically occurs in larger vessels or at high flow rates, where the blood flow becomes chaotic and irregular.

The Reynolds Number (Re), a dimensionless number, helps predict the flow regime (laminar or turbulent). A higher Re value indicates a greater likelihood of turbulent flow. The equation for Re is:

Re = ρvD / η

where:

• ρ (rho) is the density of the blood.
• v is the blood velocity.
• D is the diameter of the vessel.
• Regulation of Blood Flow:

The body has mechanisms to regulate blood flow and maintain perfusion (delivery of blood) to tissues. These mechanisms include:

• Vasoconstriction: This is the narrowing of blood vessels, reducing blood flow to a specific area. This might occur in response to cold temperatures or injury to limit blood loss.
• Vasodilation: This signifies the widening of blood vessels, increasing blood flow to a particular region. This can happen during exercise to deliver more oxygen to muscles or during digestion to direct blood flow to the digestive system.
• Autoregulation: Local mechanisms within tissues can adjust blood vessel diameter to maintain consistent blood flow despite changes in blood pressure. For example, if blood pressure increases, arterioles (small arteries) may constrict slightly to prevent excessive blood flow to the tissue.

Example: Determining Reynolds Number for Blood Flow

Imagine an artery with a diameter of 2 centimeters (cm), a blood flow velocity of 0.5 meters per second (m/s), a blood density of 1060 kg/m³, and a viscosity of 3.5 mPa·s. Let’s calculate the Reynolds Number (Re) to assess the flow regime.

Re = ρvD / η = (1060 kg/m³) × (0.5 m/s) × (0.02 m) / (3.5 × 10⁻

Applications of Fluid Dynamics in Physiology

The human body is a complex network of fluids, from the life-giving blood to the air that fuels our respiration. But how do these fluids move and interact with the intricate biological machinery? Fluid dynamics, the study of fluid motion and its forces, plays a vital role in understanding these physiological processes.

Blood Circulation: A Balancing Act

At the heart of circulation lies the concept of cardiac output, the volume of blood pumped by the heart each minute. This vital fluid needs to navigate a network of vessels with varying diameters and resistances. Here’s where Poiseuille’s Law comes in. This law describes the flow rate (Q) of a fluid through a cylindrical vessel:

Q = πΔPr^4 / (8 ηL)

where:

• Q: Flow rate (m³/s or mL/s)
• ΔP: Pressure difference between the two ends of the vessel (Pa)
• r: Radius of the vessel (m)
• η: Viscosity of the fluid (Pa·s)
• L: Length of the vessel (m)

Poiseuille’s Law tells us that the flow rate increases with a larger pressure difference, a wider vessel radius, and lower fluid viscosity. Conversely, a longer vessel or higher viscosity leads to a decrease in flow rate. This equation helps us understand how blood pressure, vessel diameter, and blood viscosity influence blood flow throughout the body.

Example: Calculating Blood Flow Rate

Imagine a blood vessel with a radius of 0.5 cm, a pressure difference of 80 mmHg (approximately 10.7 kPa), a length of 10 cm, and a blood viscosity of 3.5 mPa·s. Let’s calculate the blood flow rate (Q) using Poiseuille’s Law:

Q ≈ π × 10700 Pa × (0.005 m)⁴ / (8 × 3.5 × 10⁻³ Pa·s × 0.1 m) ≈ 1.33 × 10⁻⁶ m³/s ≈ 1.33 mL/s

This calculation suggests a blood flow rate of approximately 1.33 milliliters per second through this particular vessel.

Respiration: The Power of Pressure Gradients

Breathing relies on the movement of air into and out of the lungs. Bernoulli’s Principle explains a crucial aspect of this process. This principle states that in a flowing fluid, an increase in velocity leads to a decrease in pressure.

Imagine inhaling: As your diaphragm contracts, the volume of your chest cavity increases. This expansion creates a pressure difference between the outside air (higher pressure) and your lungs (lower pressure), causing air to flow into your lungs. Conversely, exhaling involves diaphragm relaxation, reducing lung volume and creating a pressure gradient that pushes air out.

Summary

Fluid dynamics plays a significant role in various physiological processes. By understanding concepts like viscosity, flow rate, and pressure gradients, we gain valuable insights into blood circulation, respiration, and other vital functions within the human body.

Lecture VIII: Pressure and its Applications in Biology and Medicine

Introduction to Pressure

Pressure is a fundamental concept in biology and medicine. It refers to the force exerted per unit area on a surface. In biological systems, pressure plays a crucial role in various functions, from blood flow to cell function. We’ll explore different aspects of pressure and its applications.

Blood Pressure and Its Measurement

Blood Pressure (BP): The force exerted by circulating blood on the walls of blood vessels. It’s a vital indicator of cardiovascular health. Blood pressure readings consist of two values:

• Systolic Pressure: The pressure during heart contraction (typically the higher number).
• Diastolic Pressure: The pressure during heart relaxation (typically the lower number).

Measurement of Blood Pressure:

Blood pressure is measured using a sphygmomanometer (a cuff and pressure gauge) and a stethoscope (manual method) or automated blood pressure monitors.

Procedure (Manual Method):

1. Wrap the cuff around the upper arm at heart level.
2. Inflate the cuff to restrict blood flow.
3. Gradually deflate the cuff while listening with a stethoscope.
4. Record the pressures at which Korotkoff sounds appear (systolic) and disappear (diastolic).

Blood Pressure Equation:

Pressure = Force / Area

Example:

If a person’s blood pressure is 120 mmHg systolic and 80 mmHg diastolic, what is the pressure in Pascals (Pa)?

Conversion: 1 mmHg ≈ 133.322 Pa

• Systolic pressure: 120 mmHg * 133.322 Pa/mmHg ≈ 15998.64 Pa
• Diastolic pressure: 80 mmHg * 133.322 Pa/mmHg ≈ 10665.76 Pa

Osmotic Pressure and Its Role in Cell Function

Osmotic Pressure (π): The pressure required to prevent the flow of solvent (usually water) across a semipermeable membrane into a solution. It plays a critical role in maintaining the balance of water and solutes within cells.

Van’t Hoff’s Law: This equation helps calculate osmotic pressure:

pen_spark

π = iCRT

where:

• π (pi): osmotic pressure
• i: ionization constant (depends on the solute)
• C: molar concentration of the solution
• R: gas constant (0.0821 L·atm·K⁻¹·mol⁻¹)
• T: absolute temperature (Kelvin)

Role in Cells:

Cells use osmotic pressure to regulate the movement of water and solutes across their plasma membranes. This process is essential for maintaining cell shape, volume, and various cellular functions.

Types of Solutions:

• Isotonic Solution: Has the same osmotic pressure as the cell, resulting in no net movement of water.
• Hypertonic Solution: Has a higher osmotic pressure than the cell, causing water to move out of the cell (cell shrinkage).
• Hypotonic Solution: Has a lower osmotic pressure than the cell, causing water to move into the cell (cell swelling).

Example:

Calculate the osmotic pressure of a 1 M NaCl solution at 25°C (298 K), assuming complete dissociation (i = 2 for NaCl).

π = iCRT = 2 * 1 M * 0.0821 L·atm·K⁻¹·mol⁻¹ * 298 K ≈ 48.9 atm

Centrifugation and Its Applications in Biological Research

Centrifugation: A technique that utilizes centrifugal force to separate mixtures based on the density of their components. It’s a valuable tool in separating various biological samples.

Types of Centrifugation:

• Differential Centrifugation: Separates particles based on their sedimentation rates at a constant speed.
• Density Gradient Centrifugation: Separates particles based on their density using a density gradient medium.

Principles of Centrifugation:

• Centrifugal Force (Fc): The force exerted on a particle during centrifugation. It depends on the mass (m) of the particle, the angular velocity (ω) of the rotor, and the radius (r) of rotation.

Fc = mω²r

• Sedimentation Rate: The rate at which particles settle out of a suspension during centrifugation. It’s influenced by particle size, shape, density, and the viscosity of the medium.

Applications in Biological Research:

Centrifugation is a powerful technique in biological research because it allows scientists to separate mixtures based on the density of their components. Here are some of its key applications:

Cell Fractionation:

Centrifugation is a crucial tool for separating different organelles and other cellular components from a homogenized cell lysate. By applying centrifugation at varying speeds and for different durations, researchers can isolate specific organelles like nuclei, mitochondria, or ribosomes for further analysis.

pen_spark

Purification:

Centrifugation is also used to purify various biological molecules like proteins, nucleic acids (DNA and RNA), and viruses. By employing different centrifugation techniques and density gradient mediums, researchers can isolate these molecules from complex mixtures found in cells or tissues.

Example:

Calculating Centrifugal Force:

Centrifugal force (Fc) acting on a particle during centrifugation depends on its mass (m), the angular velocity (ω) of the rotor, and the radius (r) of rotation.

Fc = mω²r

Let’s calculate the centrifugal force acting on a particle with a mass of 2 x 10⁻¹² kg in a centrifuge rotating at 10,000 rpm (revolutions per minute) with a radius of 0.1 m.

1. Convert rpm to rad/s (radians per second):

ω = 2π × (rpm) / 60

ω = 2π × (10,000 rpm) / 60 ≈ 1047.2 rad/s

2. Calculate the centrifugal force:

Fc = (2 x 10⁻¹² kg) × (1047.2 rad/s)² × (0.1 m) ≈ 2.19 x 10⁻⁶ N (Newtons)

This example demonstrates how centrifugal force increases with both particle mass and rotation speed/radius.

Summary

Understanding pressure and its applications in biology and medicine sheds light on various physiological processes:

• Blood Pressure: Measuring and interpreting systolic and diastolic pressures for cardiovascular health assessment.
• Osmotic Pressure: Understanding the movement of water across cell membranes and its impact on cell function.
• Centrifugation: Utilizing centrifugal force to separate biological components based on their density for further analysis in various research applications.

Lecture IX: Ionizing Radiation and its Interaction with Matter

Introduction

This post explores ionizing radiation, its types, and how it interacts with biological systems. Understanding ionizing radiation is critical for various applications, from medical treatments like radiotherapy to radiation safety measures.

What is Ionizing Radiation?

Ionizing radiation is high-energy radiation that can remove electrons from atoms and molecules, creating charged particles called ions. This ability to ionize matter has significant consequences in both medicine and radiation protection.

Types of Ionizing Radiation

There are three main types of ionizing radiation, each with distinct properties:

• Alpha Particles (α):
  • Composition: Alpha particles consist of two protons and two neutrons, essentially the nucleus of a helium atom.
  • Properties:
    • High mass and charge: This makes them highly ionizing but with low penetration power. A sheet of paper or even skin can stop them.
• Beta Particles (β):
  • Composition: Beta particles can be either electrons (β⁻) or positrons (β⁺), the antimatter counterpart of the electron.
  • Properties:
    • Lower mass and charge compared to alpha particles: This translates to moderate penetration (stopped by plastic or a few millimeters of tissue) and moderate ionizing power.
• Gamma Rays (γ):
  • Composition: Gamma rays are not particles, but rather high-energy electromagnetic waves (similar to light but with much higher energy).
  • Properties:
    • No mass or charge: This allows them to have high penetration power, passing through the human body and even requiring centimeters of lead for shielding.
    • Weakly ionizing compared to alpha and beta particles.

Example: Alpha Particle Decay

Here’s an example of alpha particle decay:

A nucleus of Radium-226 (²²⁶Ra) emits an alpha particle, transforming into Radon-222 (²²²Rn).

This process can be written as:

²²⁶Ra → ²²²Rn + α

In Conclusion

Understanding the different types of ionizing radiation and their properties is essential for various fields. Future posts will delve deeper into the interaction of ionizing radiation with matter and its biological effects.

Interaction of Radiation with Matter

In the previous post, we explored the different types of ionizing radiation. Now, let’s delve into how this radiation interacts with matter. Here, we’ll discuss three main processes:

1. Photoelectric Effect

Imagine a high-energy photon slamming into an atom. In the photoelectric effect, this photon gets completely absorbed by the atom, ejecting an electron in the process.

Think of it like a billiard ball (photon) hitting another ball (electron) so hard that it knocks it out of the game entirely. The photon’s energy gets transferred to the electron’s kinetic energy (the energy of movement) and the energy needed to break the electron free from the atom (binding energy).

This can be described by the following equation:

E_photon = E_binding + E_kinetic

where:

• E_photon is the energy of the incoming photon
• E_binding is the binding energy of the electron (how tightly it’s bound to the atom)
• E_kinetic is the kinetic energy of the ejected electron

2. Compton Scattering

This interaction is more like a glancing blow. Here, the photon collides with an electron, transferring only part of its energy and changing direction. The photon loses some energy in the process, which increases its wavelength (think of stretching a wave).

The amount of change in wavelength depends on the scattering angle (the angle at which the photon deflects) and can be calculated using the following equation:

Δλ = h /m_ec(1 – cosθ)

where:

• Δλ is the change in wavelength
• h is Planck’s constant (a fundamental constant in physics)
• m_e is the electron mass
• c is the speed of light
• θ is the scattering angle

3. Pair Production

For this high-energy drama, we need a powerhouse photon with energy greater than 1.022 MeV (Mega electron Volts). When such a photon interacts near an atomic nucleus, it gets completely vaporized, converting all its energy into the creation of an electron-positron pair.

Think of it as pure energy morphing into matter. The newly formed electron and its antimatter counterpart, the positron, share the initial photon’s energy, with some going into their mass and the rest as their kinetic energy.

This process is described by the equation:

E_photon = 2m_ec² + E_kinetic

where:

• E_photon is the energy of the incoming photon
• 2m_ec² is the combined rest mass energy of the electron and positron (E=mc²)
• E_kinetic is their total kinetic energy

Example: Compton Scattering in Action

Let’s say a 0.5 MeV photon scatters off an electron at a 90° angle. We can use the Compton scattering equation to calculate the change in wavelength (Δλ).

Δλ ≈ 2.43 × 10^-12 m

This tiny change highlights how the photon loses a small portion of its energy during this interaction.

Biological Effects of Ionizing Radiation

Following up on our discussion of the different types of ionizing radiation and how they interact with matter, let’s delve into how this radiation can impact living things.

1. Direct and Indirect Damage

Ionizing radiation can wreak havoc on cells in two main ways:

• Direct Damage: When radiation directly hits DNA molecules, it can break the strands, causing severe damage. Imagine a bulldozer plowing through a carefully constructed Lego model – that’s kind of what direct radiation does to DNA.
• Indirect Damage: Radiation can also ionize water molecules, which are abundant in cells. These ionized water molecules turn into free radicals, highly reactive molecules that can damage DNA and other cellular structures like loose cannons bouncing around and breaking things.

2. Deterministic Effects

These are the more predictable consequences of radiation exposure. They increase in severity with the radiation dose (the amount of radiation absorbed) and have a threshold – below a certain dose, these effects won’t occur. Examples include:

• Skin erythema (reddening)
• Radiation burns
• Cataracts

3. Stochastic Effects

These effects are trickier to predict. They can happen by chance, and the probability of them occurring increases with radiation dose, but there’s no threshold – even low doses can potentially lead to these effects. Examples include:

• Cancer
• Genetic mutations

4. Radiation Dosimetry

To quantify the biological effects of radiation exposure, we use two units:

• Gray (Gy): This measures the absorbed dose of radiation, regardless of the radiation type.
• Sievert (Sv): This considers both the absorbed dose and the biological effectiveness of the specific radiation type. Radiation weighting factors are used to account for the different types of radiation – alpha particles, for example, are more damaging than gamma rays for the same absorbed dose.

Dosimetry Calculation:

Imagine a person is exposed to 0.05 Gy of alpha particles (with a radiation weighting factor of 20). To calculate the equivalent dose in Sieverts, we multiply the absorbed dose by the weighting factor:

Equivalent dose (Sv) = Absorbed dose (Gy) × Radiation weighting factor

Equivalent dose (Sv) = 0.05 Gy × 20 = 1 Sv

This calculation tells us that the effect on the person’s body would be equivalent to receiving 1 Sievert of radiation, even though the absorbed dose was only 0.05 Gy.

Summary

Understanding the biological effects of ionizing radiation is crucial in various fields, from medicine (where radiation is used for cancer treatment) to radiation safety measures (protecting people from overexposure). By understanding the types of radiation, how they interact with matter, and the potential consequences, we can make informed decisions about how to use radiation safely and effectively.

Lecture X: Applications of Ionizing Radiation in Medicine

Introduction

This lecture explores the use of ionizing radiation in medicine, a powerful tool for diagnosis and treatment.

Ionizing Radiation in Medicine

• Definition: Ionizing radiation, with enough energy to ionize atoms or molecules, plays a vital role in medical imaging and therapy.
• Importance: It has revolutionized healthcare by enabling:
  • Accurate diagnosis of various diseases through imaging techniques.
  • Effective treatment of cancer and other conditions using radiation therapy.

Production of Radioisotopes

Radioisotopes, unstable isotopes that decay by emitting ionizing radiation, are crucial for medical imaging and therapy.

How are Radioisotopes Produced?

• Nuclear Reactors: Neutrons bombard stable isotopes, inducing radioactivity.
• Cyclotrons: Charged particles are accelerated to high energies and collide with target materials to produce radioisotopes.

Key Radioisotopes and their Uses

• Technetium-99m (⁹⁹ᵐTc): Its ideal half-life and gamma emission make it widely used in diagnostic imaging.
• Iodine-131 (¹³¹I): Used for treating thyroid cancer and hyperthyroidism.
• Fluorine-18 (¹⁸F): Employed in Positron Emission Tomography (PET) imaging.

Understanding Half-life (T₁/₂)

Half-life refers to the time it takes for half of a radioactive material to decay. The following equation describes this concept:

**N(t) = N₀ (½)^(t / T₁/₂) **

where:

• N(t) is the remaining amount of the radioisotope at time t.
• N₀ is the initial quantity.
• T₁/₂ is the half-life.

Example: Calculating Remaining Activity

If the half-life of ¹⁹⁹ᵐTc is 6 hours and its initial activity is N₀, what’s the remaining activity after 12 hours?

N(t) = N₀ (½)^(t / T₁/₂) = N₀ (½)^(12 / 6) = N₀ (½)² = N₀/4

Therefore, the remaining activity is ¼ of the initial activity.

Nuclear Medicine Techniques

1. Positron Emission Tomography (PET) Scan

• Principle: PET scans use positron-emitting radioisotopes (e.g., ¹⁸F) to generate 3D images of functional processes within the body.

The PET Scan Process:

1. The patient receives an injection of a radiotracer containing the radioisotope.
2. Positrons emitted by the radiotracer annihilate with electrons, producing gamma photons.
3. PET scanners detect these gamma photons, creating detailed images that reveal metabolic activity.

The Annihilation Process

e⁺ + e⁻ → γ + γ

During annihilation, two gamma photons (each with 511 keV energy) are produced and travel in opposite directions.

Example: PET Scan Activity

A PET scan uses ¹⁸F with a half-life of 110 minutes. If the initial activity is 10 MBq, what’s the activity after 220 minutes?

N(t) = N₀ (½)^(t / T₁/₂) = 10 MBq (½)^(220 / 110) = 10 MBq (½)² = 2.5 MBq

The activity reduces to 2.5 MBq after 220 minutes.

2. Radiation Therapy

• Principle: Radiation therapy uses high doses of ionizing radiation to damage cancer cells’ DNA, ultimately killing them.
• Types:
  • External Beam Radiation Therapy (EBRT): High-energy X-rays or gamma rays are delivered from outside the body to target the tumor.
  • Brachytherapy: Radioactive sources are placed directly inside or near the tumor.

Understanding Radiation Dose (Gy)

The dose (Gy) refers to the amount of radiation absorbed by tissue. It’s calculated using the following equation:

D = E / m

where:

• D is the dose.
• E is the absorbed energy.
• m is the mass of the tissue.

Example: Calculating Radiation Dose

If a tumor mass of 2 kg absorbs 4 J of energy, what’s the dose delivered?

D = E / m = 4 J / 2 kg = 2 Gy

The tumor receives a dose of 2 Gy.

Summary

Understanding the applications of ionizing radiation in medicine involves:

• Production of Radioisotopes: Methods of producing radioisotopes for imaging and therapy, and their properties.
• Nuclear Medicine Techniques: Principles and applications of PET scans and radiation therapy in diagnosing and treating diseases.

Course Review and Summary

This course delved into the fascinating world of biophysics, exploring how the principles of physics govern biological systems. Here’s a recap of the key takeaways:

Key Concepts:

• Ionizing Radiation: Radiation with enough energy to ionize atoms and molecules, used in medical imaging and therapy (e.g., X-rays, gamma rays).
• Radioisotopes: Unstable isotopes that decay by emitting ionizing radiation, crucial for medical applications.
• Half-life (T₁/₂): The time it takes for half of a radioactive material to decay.
• Photoelectric Effect: A photon is absorbed by an atom, ejecting an electron.
• Compton Scattering: A photon collides with an electron, transferring some of its energy and changing direction.
• Pair Production: A high-energy photon transforms into an electron-positron pair near an atomic nucleus.
• Direct vs. Indirect Damage: Radiation can directly damage DNA or indirectly damage it through the creation of free radicals from water molecules.
• Deterministic Effects: Radiation effects that increase in severity with dose and have a threshold below which they don’t occur (e.g., skin burns).
• Stochastic Effects: Radiation effects that occur by chance and increase in probability with dose, with no threshold (e.g., cancer).
• Gray (Gy): Unit of absorbed radiation dose.
• Sievert (Sv): Unit of equivalent dose, considering both absorbed dose and the radiation type’s biological effectiveness.
• Nuclear Medicine Techniques: Techniques like PET scans and radiation therapy that utilize radioisotopes for diagnosis and treatment.

Applications of Biophysics:

Biophysics is a powerful tool applied in various fields:

• Medicine: Used in medical imaging (X-rays, MRI), radiation therapy for cancer treatment, and developing new diagnostic tools.
• Pharmacology: Understanding the interaction of drugs with biological molecules at the cellular level.
• Neuroscience: Studying the electrical activity of the brain and nervous system.
• Biomechanics: Analyzing the movement of the body and the forces acting on muscles and bones.
• Bioengineering: Designing new materials and technologies for medical applications and prosthetics.

By understanding the principles of biophysics, we gain a deeper appreciation for the intricate workings of living systems and unlock possibilities for advancements in medicine, technology, and our understanding of life itself.