Hydrostatics, Pressure, Density, Buoyancy and Floatation

In the previous tutorial, we discussed Elasticity, Hooke’s Law. In this tutorial, we will discuss the following:

• Pressure and force applied to stable fluids.
• The concept of density of fluids and
• The concept of buoyancy and floatation.

Introduction

The first study about fluids was done by Archimedes, who developed some calculating methods using buoyancy of water. Leonardo daVinci made important development by developing continuum equations and nozzle flow. In frictionless flow, the most important developments were done by Daniel Bernoulli, Leoner Euler, Joseph –Loui Lagrange and Pier Simon Laplace. Osborne Reynolds improved the classical tube experiment where he found pure numbers for fluid flow.

Hydrostatics is the branch of fluid mechanics that deals with the behavior of stationary fluids (liquids and gases) at rest. It specifically focuses on the study of fluids under the influence of gravitational forces and pressure.

Key principles and concepts in hydrostatics include:

Pressure

Pressure: Pressure is a fundamental concept in hydrostatics. It refers to the force exerted by a fluid per unit area. The pressure exerted by a fluid at a given point is equal in all directions and is transmitted uniformly throughout the fluid. The magnitude of pressure at a particular point in a fluid is determined by the density of the fluid and the depth or height of the fluid column above that point.

Pascal’s Principle

Pascal’s Principle: Pascal’s principle states that when a pressure is applied to a fluid in a confined space, it is transmitted undiminished to all portions of the fluid and to the walls of the container. In other words, a change in pressure at one point in a fluid is transmitted equally to all other points in the fluid.

This principle is the basis for several important hydrostatic devices, such as hydraulic systems, hydraulic lifts, and hydraulic brakes. Pascal’s principle allows for the amplification of force by transmitting pressure through a confined fluid.

Hydrostatic Pressure and the Pressure Equation

Hydrostatic Pressure and the Pressure Equation: The hydrostatic pressure at a particular depth within a fluid is the pressure exerted by the fluid due to the weight of the fluid column above that point. The hydrostatic pressure increases with depth.

The pressure equation for hydrostatics is given by:

\[ P = \rho gh \]

Where P is the pressure at a depth h, ρ is the density of the fluid, g is the acceleration due to gravity, and h is the depth below the surface of the fluid.

This equation shows that the pressure is directly proportional to the density of the fluid, the acceleration due to gravity, and the depth of the fluid.

4. Buoyancy and Archimedes’ Principle: Buoyancy is the upward force exerted on an object immersed in a fluid. Archimedes’ principle states that the buoyant force experienced by an object immersed in a fluid is equal to the weight of the fluid displaced by the object.

This principle explains why objects float or sink in fluids. If the weight of the object is less than the weight of the fluid it displaces, the object will float. If the weight of the object is greater, it will sink.

Hydrostatic Forces on Surfaces

Hydrostatic Forces on Surfaces: In hydrostatics, the study of forces exerted by a fluid on a solid surface is of particular interest. The force exerted by a fluid on a submerged surface is perpendicular to the surface and is known as hydrostatic force.

The magnitude of the hydrostatic force on a surface depends on the pressure distribution over the surface and the area of the surface. The hydrostatic force can be determined by integrating the pressure over the surface area.

These are some of the fundamental principles and concepts in hydrostatics. They provide a framework for understanding the behavior of fluids at rest, pressure distribution, buoyancy, and the forces exerted by fluids on solid surfaces. Hydrostatics has numerous practical applications, ranging from designing structures to analyzing fluid systems and understanding natural phenomena such as buoyancy and fluid equilibrium.

Density

Density is a fundamental concept in physics that describes how much mass is packed within a given volume of a substance.

It is defined as the mass per unit volume of an object or material.
Mathematically, density (ρ) is expressed as:
Density (ρ) = Mass (m) / Volume (V)

The SI unit for density is kilograms per cubic meter (kg/m³), but other units such as grams per cubic centimeter (g/cm³) or pounds per cubic inch (lb/in³) are also commonly used.

Density is a scalar quantity that provides valuable information about the compactness and concentration of mass within a substance. It allows for the comparison of different materials and the determination of their behavior under various conditions.

Some key points about density include:

1. Relationship between Mass, Volume, and Density: Density is directly proportional to mass and inversely proportional to volume. This means that if the mass of an object increases while the volume remains constant, the density also increases. Conversely, if the volume increases while the mass remains constant, the density decreases.
2. Determining Mass or Volume from Density: Using the density equation, we can rearrange it to find either the mass or the volume of an object, given the other two variables:

Mass (m) = Density (ρ) × Volume (V)

Volume (V) = Mass (m) / Density (ρ)

These equations are useful for calculating the mass or volume of a substance when the density is known.

3. Density and Floating/Sinking: The concept of density is particularly important when considering the behavior of objects in fluids. An object will float if its density is less than the density of the fluid it is placed in, and it will sink if its density is greater than the density of the fluid. This principle is evident in phenomena like buoyancy and the Archimedes’ principle.
4. Density and Material Identification: Density is a characteristic property of substances and can be used to identify or differentiate materials. Different materials have different densities, and this property can be helpful in fields such as material science, geology, and forensics.
5. Temperature and Pressure Effects: Density is influenced by temperature and pressure changes. As temperature increases, the volume of a substance generally expands, leading to a decrease in density. Changes in pressure can also affect the density of gases and liquids.

It’s important to note that the density of a substance may vary with temperature and pressure, particularly for gases and liquids. In such cases, it is common to specify the reference temperature and pressure at which the density is measured.

Overall, density provides valuable information about the mass distribution and compactness of a material. It is a fundamental property used in various scientific and engineering applications, including material characterization, fluid dynamics, and determining the behavior of objects in different environments.

Problem 1: A cube of material has a volume of 100 cm³ and a mass of 500 grams. Calculate the density of the material.

Solution: Density is defined as mass (m) divided by volume (V). In this problem, we have the mass and volume given, so we can use the formula:

Density (ρ) = Mass (m) / Volume (V)

Given: Mass (m) = 500 grams Volume (V) = 100 cm³

Converting the mass to kilograms: Mass (m) = 500 grams = 500/1000 = 0.5 kg

Converting the volume to cubic meters: Volume (V) = 100 cm³ = 100/1000000 = 0.0001 m³

Now we can calculate the density: Density (ρ) = 0.5 kg / 0.0001 m³ = 5000 kg/m³

Therefore, the density of the material is 5000 kg/m³.

Problem 2: A sphere has a density of 2.5 g/cm³ and a radius of 5 cm. calculate its mass.

Solution: The formula for the volume of a sphere is given by V = (4/3) * π * r³, where r is the radius.

Given: Density (ρ) = 2.5 g/cm³ Radius (r) = 5 cm

Converting the density to kg/m³: Density (ρ) = 2.5 g/cm³ = 2.5 * 1000 kg/m³ = 2500 kg/m³

Converting the radius to meters: Radius (r) = 5 cm = 5/100 = 0.05 m

Using the formula for volume: Volume (V) = (4/3) * π * (0.05)³ = 0.0005236 m³

Now we can calculate the mass using the formula for density: Mass (m) = Density (ρ) * Volume (V) = 2500 kg/m³ * 0.0005236 m³ = 1.309 kg

Therefore, the mass of the sphere is approximately 1.309 kg.

Specific gravity

Specific gravity is a dimensionless quantity that compares the density of a substance to the density of a reference substance. It provides a relative measure of how dense a substance is compared to another substance. The reference substance used for comparison is typically water, which has a specific gravity of 1.

Specific gravity (SG) is defined as the ratio of the density of a substance (ρ) to the density of the reference substance (ρ₀):

Specific Gravity (SG) = Density of Substance (ρ) / Density of Reference Substance (ρ₀)

Since specific gravity is a ratio of densities, it is a unitless quantity.

The specific gravity of a substance provides useful information about its buoyancy and density in comparison to water. Here are a few key points to note about specific gravity:

1. Relationship to Density: Specific gravity is directly related to density. If the density of a substance is greater than the density of the reference substance (e.g., water), its specific gravity will be greater than 1. Conversely, if the density of a substance is lower than the density of the reference substance, its specific gravity will be less than 1.
2. Buoyancy: Specific gravity is often used to determine the buoyancy of objects in a fluid. An object with a specific gravity greater than 1 will sink in the fluid, while an object with a specific gravity less than 1 will float. For example, if the specific gravity of a liquid is 1.5, it means the liquid is 1.5 times as dense as water and any object with a specific gravity greater than 1.5 will sink in that liquid.
3. Comparison of Substances: Specific gravity allows for the easy comparison of densities between different substances. For example, if you have two different liquids and you want to know which one is denser, you can compare their specific gravities. The substance with the higher specific gravity will be denser.
4. Temperature Dependency: It’s important to note that specific gravity can be temperature-dependent, especially for substances that exhibit significant volume changes with temperature. Therefore, it is crucial to specify the temperature at which the specific gravity is measured or take temperature corrections into account when comparing specific gravities.
5. Application: Specific gravity finds applications in various fields, such as materials science, chemistry, geology, and engineering. It is used to determine the concentration of solutions, assess the purity of substances, analyze the composition of materials, and characterize the properties of liquids, gases, and solids.

To summarize, specific gravity provides a relative measure of density by comparing the density of a substance to the density of a reference substance (usually water). It helps determine buoyancy, compare densities between substances, and has various practical applications in different fields.

Problem 1: A liquid has a density of 1200 kg/m³. Calculate its specific gravity.

Solution: Specific gravity is defined as the ratio of the density of a substance to the density of a reference substance. In most cases, the reference substance used for liquids is water. Therefore, the specific gravity can be calculated using the formula:

Specific Gravity = Density of Substance / Density of Water

Given: Density of Substance = 1200 kg/m³ Density of Water = 1000 kg/m³

Using the provided values, we can calculate the specific gravity:

Specific Gravity = 1200 kg/m³ / 1000 kg/m³ = 1.2

Therefore, the specific gravity of the liquid is 1.2.

Problem 2: A solid has a specific gravity of 0.8 and a density of 8000 kg/m³. Calculate the density of the reference substance.

Solution: To calculate the density of the reference substance, we can rearrange the formula for specific gravity:

Specific Gravity = Density of Substance / Density of Water

Rearranging the formula:

Density of Water = Density of Substance / Specific Gravity

Given: Specific Gravity = 0.8 Density of Substance = 8000 kg/m³

Using the provided values, we can calculate the density of the reference substance:

Density of Water = 8000 kg/m³ / 0.8 = 10000 kg/m³

Therefore, the density of the reference substance (water in this case) is 10000 kg/m³.

These are just a couple of examples of how to solve problems involving specific gravity. Remember to use the appropriate formulas and apply the relevant values based on the given data.

Pressure in Fluids

Pressure in fluids refers to the force exerted per unit area on a surface by the fluid. It is a fundamental concept in fluid mechanics and plays a crucial role in understanding the behavior of fluids, including liquids and gases. Pressure is responsible for various phenomena, such as buoyancy, fluid flow, and the transmission of forces in fluids.

Pressure is defined mathematically as: Pressure (P) = Force (F) / Area (A)

\[ P = \frac{F}{A} \]

Where the force is perpendicular to the surface over which it acts, and the area is the surface on which the force is applied. The SI unit for pressure is the Pascal (Pa), which is equal to one newton per square meter (N/m²).

There are a few important principles and concepts related to pressure in fluids:

1. Pascal’s Law: Pascal’s law states that pressure applied to a fluid in a closed container is transmitted equally in all directions. This means that the pressure at any point within a fluid in equilibrium is the same in all directions. It allows the use of hydraulic systems, where pressure applied to a small area can be used to create a larger force on a larger area.
2. Hydrostatic Pressure: Hydrostatic pressure refers to the pressure exerted by a fluid at rest due to the weight of the fluid above it. In a column of fluid, the pressure at any given depth increases with the weight of the fluid above that point. The hydrostatic pressure depends on the density of the fluid, acceleration due to gravity, and the height or depth of the fluid.
3. Gauge Pressure and Absolute Pressure: Gauge pressure is the pressure measured relative to atmospheric pressure. It is the difference between the actual pressure and atmospheric pressure. Absolute pressure, on the other hand, is the total pressure including atmospheric pressure. Absolute pressure is often used in calculations and is measured with reference to a vacuum.
4. Pressure in Fluids at Different Depths: The pressure in a fluid at different depths can be calculated using the equation:

Pressure (P) = Pressure at the surface + ρgh

Where ρ is the density of the fluid, g is the acceleration due to gravity, and h is the depth or height of the fluid.

5. Applications of Pressure in Fluids: Pressure in fluids has various practical applications. Some examples include:

• Hydraulic systems: The principles of pressure in fluids are used in hydraulic systems, which are widely used in machinery and vehicles for transmitting forces.
• Barometers: Barometers measure atmospheric pressure and are used in weather forecasting.
• Blood pressure: Blood pressure measurement is based on the pressure exerted by blood on the walls of blood vessels.
• Diving and scuba diving: Understanding pressure in fluids is crucial for divers to prevent decompression sickness and understand the effects of pressure on the body underwater.

Understanding pressure in fluids is essential for analyzing fluid behavior, designing hydraulic systems, predicting fluid flow, and studying various phenomena in fluid mechanics.

Problem 1: A water tank has a depth of 5 meters. Calculate the pressure exerted by the water at the bottom of the tank.

Solution: The pressure exerted by a fluid at a certain depth can be calculated using the formula:

Pressure (P) = Density (ρ) * Acceleration due to gravity (g) * Height (h)

Given: Depth (h) = 5 meters Density of water (ρ) = 1000 kg/m³ (approximate value) Acceleration due to gravity (g) = 9.8 m/s²

Using the given values, we can calculate the pressure:

Pressure (P) = 1000 kg/m³ * 9.8 m/s² * 5 m = 49,000 Pa or 49 kPa

Therefore, the pressure exerted by the water at the bottom of the tank is approximately 49 kPa.

Problem 2: A scuba diver is 20 meters underwater. Calculate the pressure exerted by the water at that depth.

Solution: Similar to the previous problem, we can calculate the pressure using the formula:

Pressure (P) = Density (ρ) * Acceleration due to gravity (g) * Depth (h)

Given: Depth (h) = 20 meters Density of water (ρ) = 1000 kg/m³ (approximate value) Acceleration due to gravity (g) = 9.8 m/s²

Using the given values, we can calculate the pressure:

Pressure (P) = 1000 kg/m³ * 9.8 m/s² * 20 m = 196,000 Pa or 196 kPa

Therefore, the pressure exerted by the water at a depth of 20 meters is approximately 196 kPa.

Pascal’s Principle

Pascal’s principle, also known as Pascal’s law, is a fundamental principle in fluid mechanics named after the French mathematician and physicist Blaise Pascal. It states that when there is an increase in pressure at any point in an enclosed fluid, the pressure is transmitted undiminished to all other parts of the fluid and to the walls of its container. In simpler terms, a change in pressure applied to a fluid in a confined space will propagate uniformly in all directions.

Key points regarding Pascal’s principle:

1. Pressure Transmission: According to Pascal’s principle, a change in pressure exerted at one point in a fluid will be transmitted throughout the fluid without loss. This is because fluids are considered to be incompressible, meaning they do not easily change their volume under pressure.
2. Equal Magnitude: The transmitted pressure is equal in magnitude in all directions. Whether the pressure is increased or decreased at a particular point, the change is distributed uniformly throughout the fluid. This principle holds true for both liquid and gas fluids.
3. Hydraulic Systems: Pascal’s principle finds significant application in hydraulic systems. A hydraulic system uses an incompressible fluid (usually oil or water) to transmit force from one point to another. By applying a small force on a small piston (known as the input piston) connected to a larger piston (known as the output piston) through an enclosed fluid, a much larger force can be generated at the output piston. This multiplication of force is based on the principle of pressure transmission.
4. Hydraulic Lifts and Brakes: Pascal’s principle is utilized in various practical applications. Hydraulic lifts, for example, use the principle to lift heavy loads by applying a small force on a small piston, resulting in a larger force lifting the load. Hydraulic brakes in vehicles also use Pascal’s principle to amplify the force applied by the driver’s foot on the brake pedal, allowing effective braking of the vehicle.
5. Applications in Science and Engineering: Pascal’s principle is essential in understanding various phenomena in fluid mechanics, such as fluid pressure, fluid flow, buoyancy, and hydrostatics. It is widely applied in fields like engineering, aviation, automotive technology, and hydraulic machinery design.

Pascal’s principle provides a fundamental understanding of the behavior of fluids under pressure and allows engineers and scientists to design and optimize various systems that rely on fluid transmission of force. It is a key principle that enables the efficient functioning of hydraulic systems and finds practical applications in numerous aspects of our daily lives.

To derive the equations related to Pascal’s principle, let’s consider a simple setup of a fluid confined within a container connected to two pistons. One piston has a smaller cross-sectional area (A₁), while the other has a larger cross-sectional area (A₂).

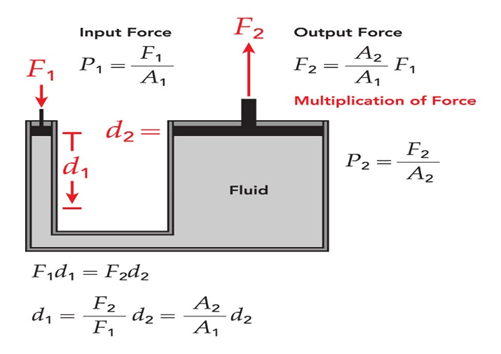
1. Pressure Equation: According to Pascal’s principle, the pressure change is transmitted equally throughout the fluid. Therefore, the pressure at any point within the fluid is the same. We can express this as:

Pressure at point 1 = Pressure at point 2

P₁ = P₂

2. Force Equation: To relate the force exerted by the fluid on each piston, we can use the definition of pressure as force divided by area.

Force (F₁) = Pressure (P₁) * Area (A₁)

Force (F₂) = Pressure (P₂) * Area (A₂)

Since P₁ = P₂ (as per Pascal’s principle), we can rewrite the equations as:

Force (F₁) = Pressure (P) * Area (A₁)

Force (F₂) = Pressure (P) * Area (A₂)

3. Relationship between Forces and Areas: Using the above equations, we can derive a relationship between the forces exerted by the fluid on the pistons:

F₁ / A₁ = F₂ / A₂

This equation shows that the ratio of the force exerted by the fluid to the area of the piston is the same for both pistons. In other words, the force exerted by the fluid is directly proportional to the piston’s cross-sectional area.

These equations demonstrate the fundamental principles of Pascal’s law. They show that when a pressure is applied to a fluid in a confined container, the pressure change is transmitted equally throughout the fluid, and the force exerted by the fluid on any piston is determined by the pressure and the piston’s cross-sectional area.

Problem 1: A hydraulic lift system has a small piston with a radius of 5 cm and a large piston with a radius of 20 cm. If a force of 200 N is applied to the small piston, calculate the force exerted by the large piston.

Solution: According to Pascal’s principle, the pressure is transmitted equally in all directions within a confined fluid. Therefore, the pressure exerted on the small piston is equal to the pressure exerted on the large piston.

Given: Radius of the small piston (r1) = 5 cm = 0.05 m Radius of the large piston (r2) = 20 cm = 0.20 m Force applied to the small piston (F1) = 200 N

Using the formula for pressure (P = Force / Area), we can calculate the force exerted by the large piston (F2):

Pressure on small piston (P1) = Pressure on large piston (P2) F1 / A1 = F2 / A2

The area of a piston can be calculated using the formula: A = π * r²

A1 = π * (0.05 m)² A2 = π * (0.20 m)²

Since the pressure is equal, we have: F1 / (π * (0.05 m)²) = F2 / (π * (0.20 m)²)

Simplifying the equation: F2 = F1 * (A2 / A1) F2 = 200 N * ((π * (0.20 m)²) / (π * (0.05 m)²)) F2 = 200 N * (0.20 m)² / (0.05 m)² F2 = 200 N * 16 F2 = 3200 N

Therefore, the force exerted by the large piston is 3200 N.

Problem 2: A hydraulic press is used to lift a heavy object. The input piston has a radius of 10 cm and the output piston has a radius of 40 cm. If a force of 5000 N is applied to the input piston, calculate the force exerted on the object.

Solution: Following Pascal’s principle, the pressure exerted on the input piston is transmitted equally to the output piston and the object being lifted.

Given: Radius of the input piston (r1) = 10 cm = 0.10 m Radius of the output piston (r2) = 40 cm = 0.40 m Force applied to the input piston (F1) = 5000 N

Using the formula for pressure, we can determine the force exerted on the object (F2):

Pressure on input piston (P1) = Pressure on output piston (P2) F1 / A1 = F2 / A2

The area of a piston can be calculated using the formula: A = π * r²

A1 = π * (0.10 m)² A2 = π * (0.40 m)²

Since the pressure is equal, we have: F1 / (π * (0.10 m)²) = F2 / (π * (0.40 m)²)

Simplifying the equation: F2 = F1 * (A2 / A1) F2 = 5000 N * ((π * (0.40 m)²) / (π * (0.10 m)²)) F2 = 5000 N * (0.40 m)² / (0.10 m)² F2 = 5000 N * 16 F2 = 80000 N

Therefore, the force exerted on the object is 80000 N.

Viscosity

Viscosity is a fundamental property of fluids that describes their resistance to flow or deformation under the influence of an external force. It is a measure of the internal friction within a fluid as it moves or flows. Viscosity plays a crucial role in various scientific disciplines, including physics, chemistry, engineering, and biology.

1. Definition: Viscosity is defined as the ratio of shear stress to shear rate. Shear stress represents the force per unit area acting parallel to the direction of flow within the fluid, while shear rate represents the rate at which layers of the fluid slide past each other. Mathematically, viscosity (η) can be expressed using the equation:

η = Shear Stress / Shear Rate  

\[ \eta = \frac{\frac{F}{A}}{\frac{v}{l}} \]

Where

Where v = speed, l = distance, F = force, and A = area.

Viscosity is typically measured in pascal-seconds (Pa·s) or poise (P), where 1 P = 0.1 Pa·s.

2. Types of Viscosity: There are two primary types of viscosity:

• Dynamic (or absolute) Viscosity: Dynamic viscosity refers to the resistance to flow of a fluid when subjected to a shearing force. It is the ratio of shear stress to shear rate and is commonly denoted by the symbol η. Fluids with higher dynamic viscosity flow more slowly, while fluids with lower dynamic viscosity flow more easily. Examples of fluids with high dynamic viscosity include honey and molasses, while examples of fluids with low dynamic viscosity include water and gasoline.
• Kinematic Viscosity: Kinematic viscosity is the ratio of dynamic viscosity to the density of the fluid. It provides a measure of how easily a fluid flows under the influence of gravity. Kinematic viscosity is denoted by the symbol ν and is given by the equation:

ν = Dynamic Viscosity / Density

Kinematic viscosity is often used in fluid mechanics calculations, particularly in applications involving the motion of fluids through pipes or channels.

3. Temperature Dependence: Viscosity is strongly influenced by temperature. In general, as temperature increases, the viscosity of most liquids decreases, making them flow more easily. This behavior is due to the increased molecular motion at higher temperatures, which reduces the internal friction within the fluid. However, for some fluids, such as non-Newtonian fluids, the relationship between temperature and viscosity can be more complex.
4. Newtonian and Non-Newtonian Fluids: Viscosity can be classified based on the flow behavior of fluids:

• Newtonian Fluids: Newtonian fluids exhibit a linear relationship between shear stress and shear rate. The viscosity remains constant regardless of the applied shear stress. Examples of Newtonian fluids include water, gasoline, and most gases.
• Non-Newtonian Fluids: Non-Newtonian fluids do not follow a linear relationship between shear stress and shear rate. Their viscosity can change with the applied shear stress or shear rate. Non-Newtonian fluids can exhibit shear-thinning behavior (decrease in viscosity with increasing shear rate) or shear-thickening behavior (increase in viscosity with increasing shear rate). Examples of non-Newtonian fluids include ketchup, toothpaste, and polymer solutions.

5. Applications: Viscosity has numerous practical applications across various fields:

• Industrial Processes: Viscosity is crucial in industrial processes that involve fluid flow, such as oil refining, chemical manufacturing, and food processing. Understanding and controlling viscosity is essential for optimizing efficiency and product quality.
• Lubrication: Viscosity is critical in lubrication applications, where it determines the ability of lubricants to reduce friction and wear between moving parts. Lubricants with appropriate viscosity help to ensure smooth operation and prevent damage in machines and engines.
• Medicine and Biotechnology: Viscosity plays a role in blood circulation, drug formulation, and the behavior of biological fluids. It affects the flow of fluids in blood vessels and the delivery of drugs within the body.
• Environmental Sciences: Viscosity influences the movement and behavior of fluids in natural systems, such as groundwater flow, ocean currents, and atmospheric processes.
• Material Science: Viscosity is relevant in the study of materials like polymers, paints, and adhesives, where it affects their processing, coating, and bonding properties.

Understanding and controlling viscosity is essential in various engineering and scientific applications to ensure optimal performance, efficiency, and safety.

Top of Form

Problem 1: A fluid has a viscosity of 0.1 Pa·s and is subjected to a shear stress of 5 Pa. Calculate the shear rate.

Solution: The shear rate (γ) is defined as the rate at which layers of a fluid move relative to each other under the applied shear stress. It is related to the shear stress (τ) and the viscosity (η) of the fluid by the following formula:

Shear rate (γ) = Shear stress (τ) / Viscosity (η)

Given: Viscosity (η) = 0.1 Pa·s Shear stress (τ) = 5 Pa

Calculating the shear rate: Shear rate (γ) = 5 Pa / 0.1 Pa·s = 50 s⁻¹ or 50 inverse seconds

Therefore, the shear rate of the fluid is 50 s⁻¹ or 50 inverse seconds.

Problem 2: A liquid flows through a pipe with a velocity gradient of 0.05 s⁻¹. If the viscosity of the liquid is 0.02 Pa·s, calculate the shear stress exerted on the walls of the pipe.

Solution: The shear stress (τ) exerted on the walls of the pipe is related to the velocity gradient (du/dy) and the viscosity (η) of the liquid by the following formula:

Shear stress (τ) = Viscosity (η) * Velocity gradient (du/dy)

Given: Viscosity (η) = 0.02 Pa·s Velocity gradient (du/dy) = 0.05 s⁻¹

Calculating the shear stress: Shear stress (τ) = 0.02 Pa·s * 0.05 s⁻¹ = 0.001 Pa or 1 mPa

Therefore, the shear stress exerted on the walls of the pipe is 0.001 Pa or 1 mPa.

Buoyancy and Archimedes Principle

Buoyancy is the upward force exerted on an object immersed in a fluid (liquid or gas) due to the pressure difference between the top and bottom of the object. It is the reason why objects float or feel lighter when submerged in a fluid. Buoyancy is a result of the fluid exerting greater pressure at deeper depths, which pushes the object upwards.

Archimedes’ Principle: Archimedes’ Principle is a fundamental principle in fluid mechanics named after the ancient Greek mathematician and physicist, Archimedes. It states that when an object is immersed in a fluid, it experiences an upward buoyant force equal to the weight of the fluid displaced by the object. This principle explains why objects float or sink in a fluid.

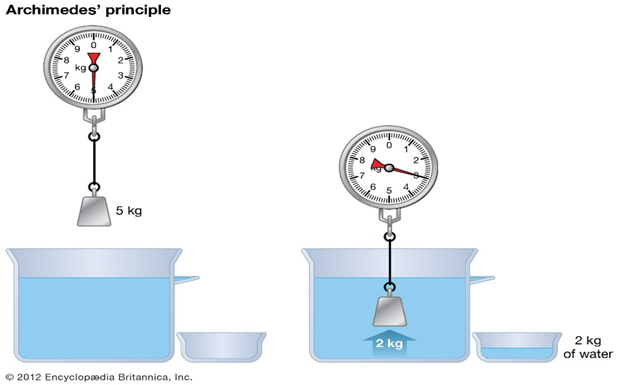
Key Points of Archimedes’ Principle:

1. Buoyant Force: Archimedes’ Principle states that the buoyant force (F_b) acting on an object immersed in a fluid is equal to the weight of the fluid displaced by the object. Mathematically, it is given by:

\[ F_b = \rho \times V \times g \]

Where ρ is the density of the fluid, V is the volume of the fluid displaced by the object, and g is the acceleration due to gravity.

2. Buoyancy and Weight: If the weight of an object is less than the buoyant force acting on it, the object will float. If the weight is greater than the buoyant force, the object will sink.
3. Apparent Weight: When an object is submerged in a fluid, it experiences a reduction in its apparent weight. The apparent weight of an object in a fluid is the difference between the object’s actual weight and the buoyant force acting on it.
4. Archimedes’ Principle and Density: Archimedes’ Principle is also useful in determining the density of an object. By comparing the apparent weight of an object in air and in a fluid, the density of the object can be calculated. If the density of the object is greater than the fluid, it will sink. If the density is less than the fluid, it will float.

Applications of Archimedes’ Principle:

1. Ship and Submarine Design: Archimedes’ Principle is crucial in designing ships and submarines to ensure their buoyancy and stability in water.
2. Hot Air Balloons: Hot air balloons utilize Archimedes’ Principle to achieve lift. The heated air inside the balloon is less dense than the surrounding air, creating a buoyant force that lifts the balloon.
3. Density Measurements: Archimedes’ Principle is used to measure the density of irregularly shaped objects by measuring the change in apparent weight when submerged in a fluid.

In summary, Archimedes’ Principle explains the buoyant force experienced by objects immersed in a fluid. It is a fundamental principle in fluid mechanics and has various practical applications.

Problem 1: A solid cube of iron with a side length of 10 cm is fully submerged in water. Determine the buoyant force acting on the cube and the apparent weight of the cube in water. The density of iron is 7.8 g/cm³, and the density of water is 1 g/cm³.

Solution: The buoyant force (F_b) acting on the cube can be calculated using Archimedes’ principle, which states that the buoyant force is equal to the weight of the fluid displaced by the submerged object. The apparent weight (W_app) of the cube in water is the difference between its weight in air and the buoyant force.

Given: Side length of the cube (l) = 10 cm Density of iron (ρ_iron) = 7.8 g/cm³ Density of water (ρ_water) = 1 g/cm³

Calculating the volume of the cube: Volume (V) = l³ = (10 cm)³ = 1000 cm³

Calculating the buoyant force: The volume of water displaced by the cube is equal to its volume: V_displaced = V = 1000 cm³

The buoyant force is given by: F_b = ρ_water x g x V_displaced

where g is the acceleration due to gravity (approximately 9.8 m/s²).

Converting the volume to liters (1 liter = 1 dm³ = 1000 cm³): V_displaced = 1000 cm³ = 1 liter

Calculating the buoyant force:  = (1 g/cm³) * (9.8 m/s²) * (1 liter) = 9.8N

Calculating the weight of the cube in air F_b: Weight (W) = mass (m) * g

Converting the density of iron to kg/m³:  ρ_iron = 7.8 g/cm³ = 7800 kg/m³

Calculating the mass of the cube: Mass (m) = ρ_iron* V = (7800 kg/m³) * (0.001 m³) = 7.8 kg

Calculating the weight of the cube in air: W = 7.8 kg * (9.8 m/s²) = 76.44 N

Calculating the apparent weight of the cube in water: Apparent weight Wapp = W–F_b = 76.44N – 9.8N = 66.64N

Therefore, the buoyant force acting on the cube is 9.8N, and the apparent weight of the cube in water is 66.64N.

Problem 2: A ship floats in seawater with a volume of 5000 m³. If the density of seawater is 1025 kg/m³, calculate the buoyant force acting on the ship.

Solution: Using Archimedes’ principle, we can determine the buoyant force acting on the ship, which is equal to the weight of the seawater displaced by the ship.

Given: Volume of the ship (V) = 5000 m³ Density of seawater (ρ_seawater) = 1025 kg/m³

Calculating the buoyant force: The buoyant force is given by: ρ_seawater x g x

where g is the acceleration due to gravity (approximately 9.8 m/s²).

Calculating the buoyant force: F_b= (1025 kg/m³) *(9.8 m/s²) *(5000 m³) = 50350000 N

Therefore, the buoyant force acting on the ship is approximately 50,350,000N.